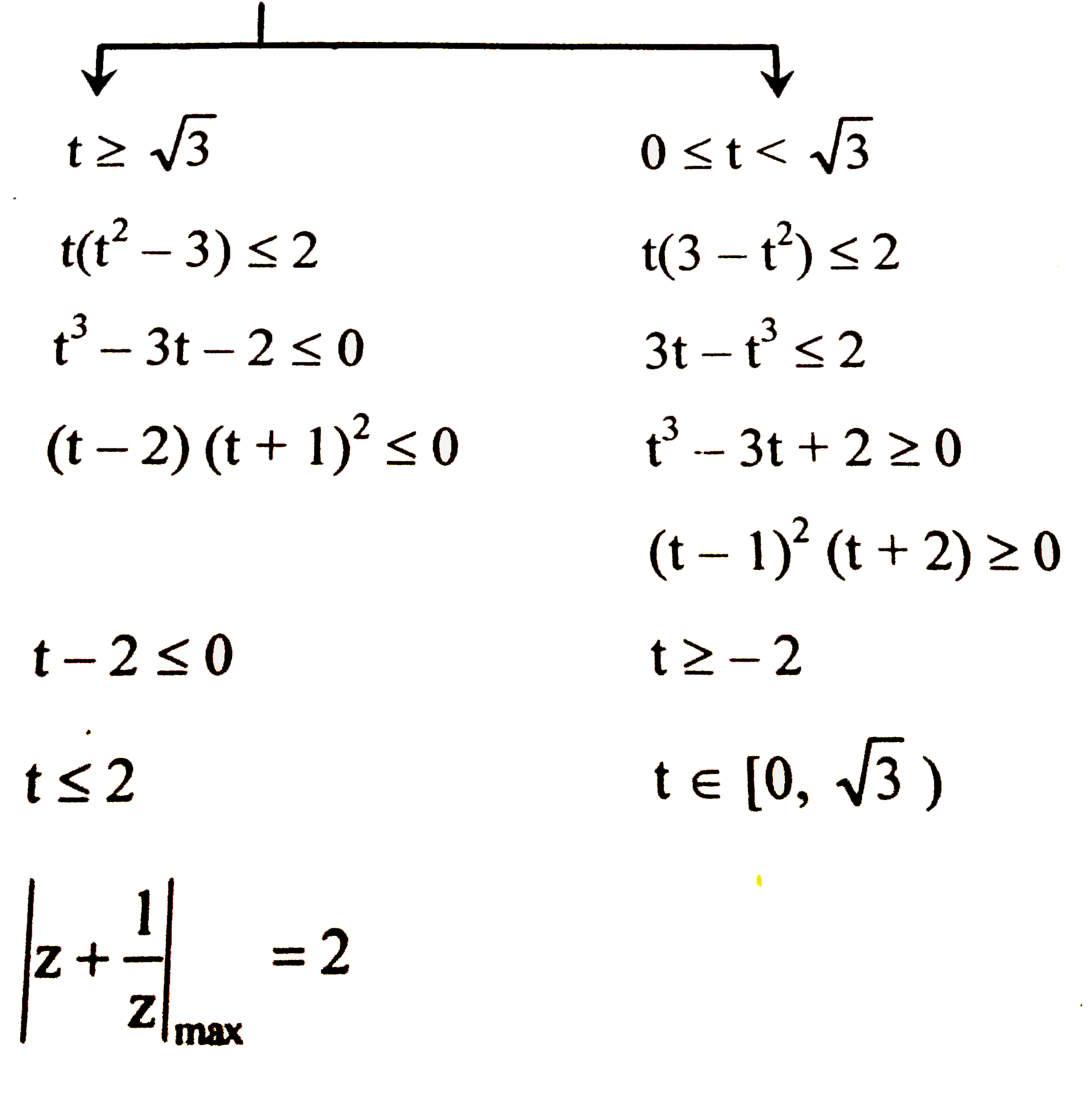A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If z a complex number satisfying |z^(3)+z^(-3)|le2, then the maximum p...
Text Solution
|
- Number of values of z (real or complex) simultaneously satisfying the ...
Text Solution
|
- The number of values of z (real or complex) e simultaneously satisfyin...
Text Solution
|
- Let z be a complex number of maximum amplitude satisfying |z-3|=Re(z),...
Text Solution
|
- If z is a complex number satisfying z^(4)+z^(3)+2z^(2)+z+1=0 then the ...
Text Solution
|
- If z a complex number satisfying |z^(3)+z^(-3)|le2, then the maximum p...
Text Solution
|
- यदि कोई सम्मिश्र संख्या z,|z-3-2i|le2 को संतुष्ट कर रहा है तब |2z-6+5i...
Text Solution
|
- Find the complex number z with maximum and minimum possible values of ...
Text Solution
|
- If the complex number z follows that |z^3+z^(-3)|le 2 , If satisfied |...
Text Solution
|