A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
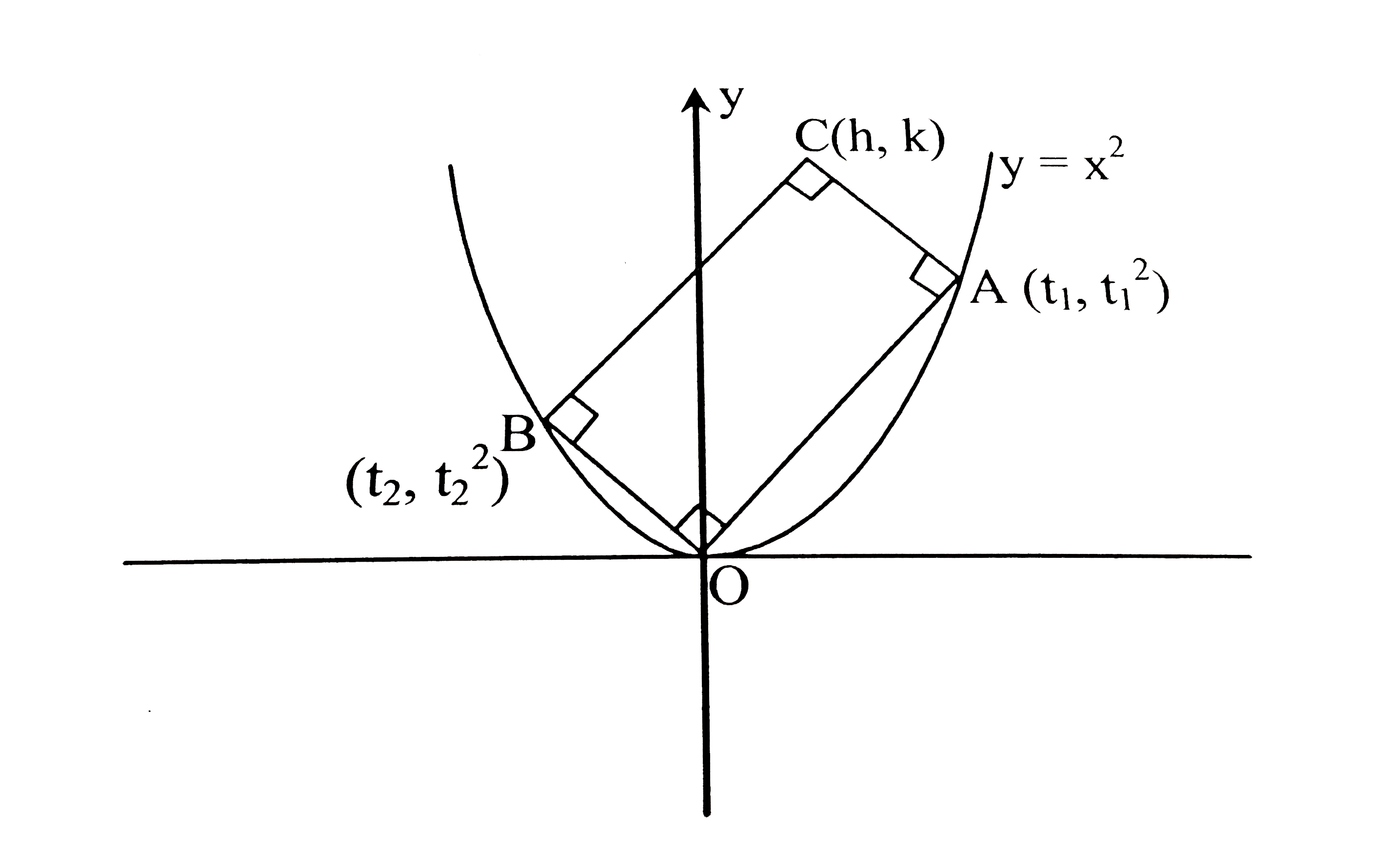
- Suppose OABC is a reatangle in the xy-plane where O is the origin and ...
Text Solution
|
- Given four points P1,P2,P3a n dP4 on the coordinate plane with origin ...
Text Solution
|
- Prove that points of the curve y^(2)=4a{x+a sin((x)/(a))} at which tan...
Text Solution
|
- Let a parabola be y=12-x^2. Find the maximum area of rectangle whose b...
Text Solution
|
- Suppose OABC is a reatangle in the xy-plane where O is the origin and ...
Text Solution
|
- सिद्ध कीजिए कि वर्क y^(2)=4a{x+a sin ((x)/(a))} के वें बिन्दु जिन पर ख...
Text Solution
|
- एक समचतुर्भुज OABC के तीन शीर्ष A, B और C,केंद्र O के वृत्त पर स्थित ...
Text Solution
|
- If axis of the parabola lie along y-axis and if vertex is at a distanc...
Text Solution
|
- Let a parabola be y=12-x^2. Find the maximum area of rectangle whose b...
Text Solution
|