A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
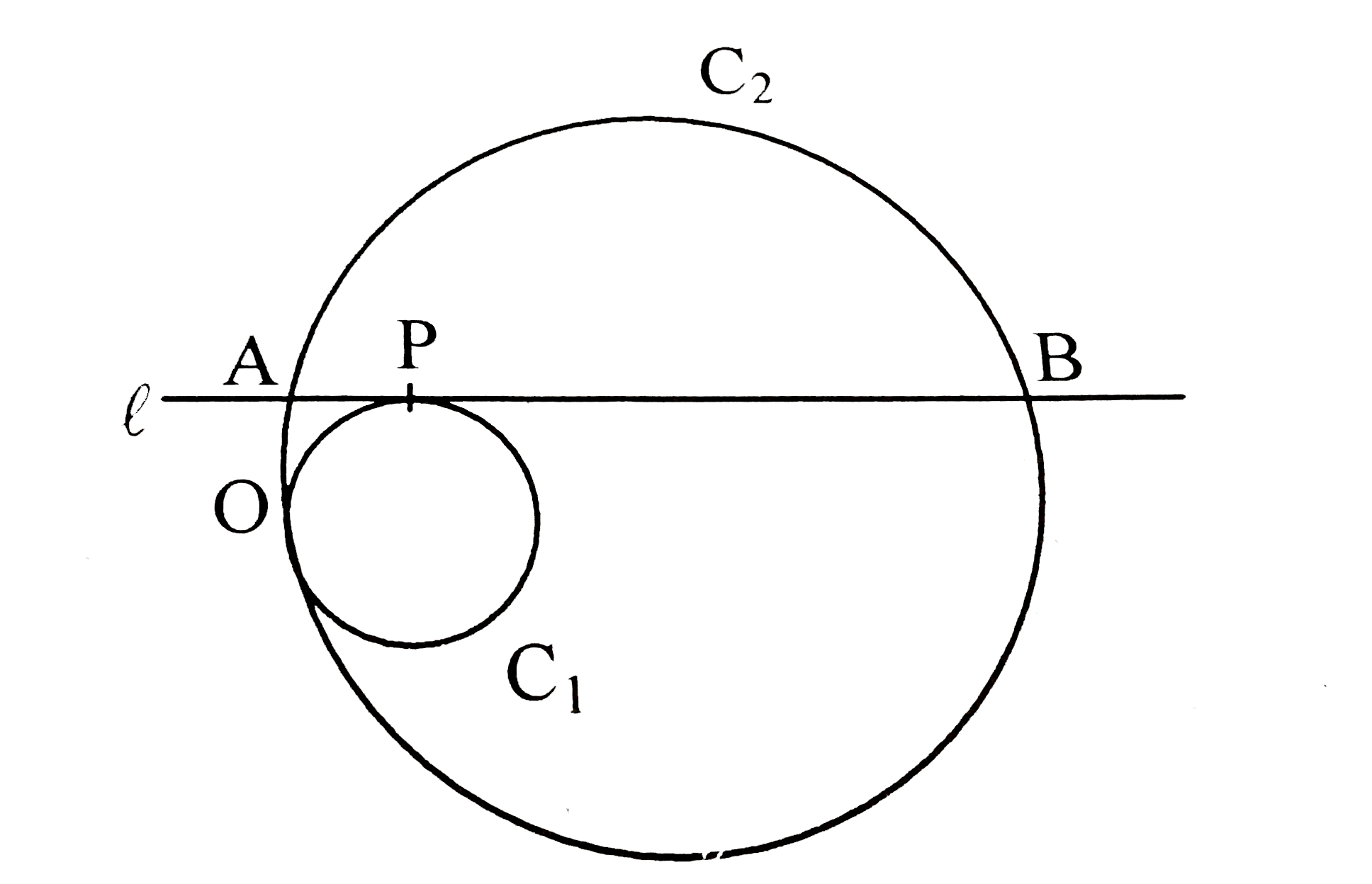
- Circles C(1) and C(2) of radii r and R respectively, touch each other ...
Text Solution
|
- Circles C(1) and C(2) of radii r and R respectively, touch each other ...
Text Solution
|
- If nger, then ""^(r)C(r)+""^(r+1)C(r)+""^(r+2)C(r)+......+""^(n)C(r)...
Text Solution
|
- |{:(.^(x)C(r),,.^(x)C(r+1),,.^(x)C(r+2)),(.^(y)C(r),,.^(y)C(r+1),,.^(y...
Text Solution
|
- |(.^(x)C(r),.^(x)C(r+1),.^(y)C(r+2)),(.^(y)C(r),.^(x)C(r+1),.^(y)C(r+2...
Text Solution
|
- Prove that - |(.^(x)C(y),.^(x)C(r+1),.^(x)C(r+2)),(.^(y)C(r),.^(y)C(r+...
Text Solution
|
- ""^(n-2)C(r)+2""^(n-2)C(r-1)+""^(n-2)C(r-2) equals :
Text Solution
|
- सिध्द कीजिए कि - C(0)C(r)+C(1)C(r+1)+C(2)C(r+2)+....+C(n-r)C(n)=((2n...
Text Solution
|
- ""^(n-2)C(r)+2.""^(n-2)C(r-1)+""^(n-2)C(r-2) is equal to
Text Solution
|