A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
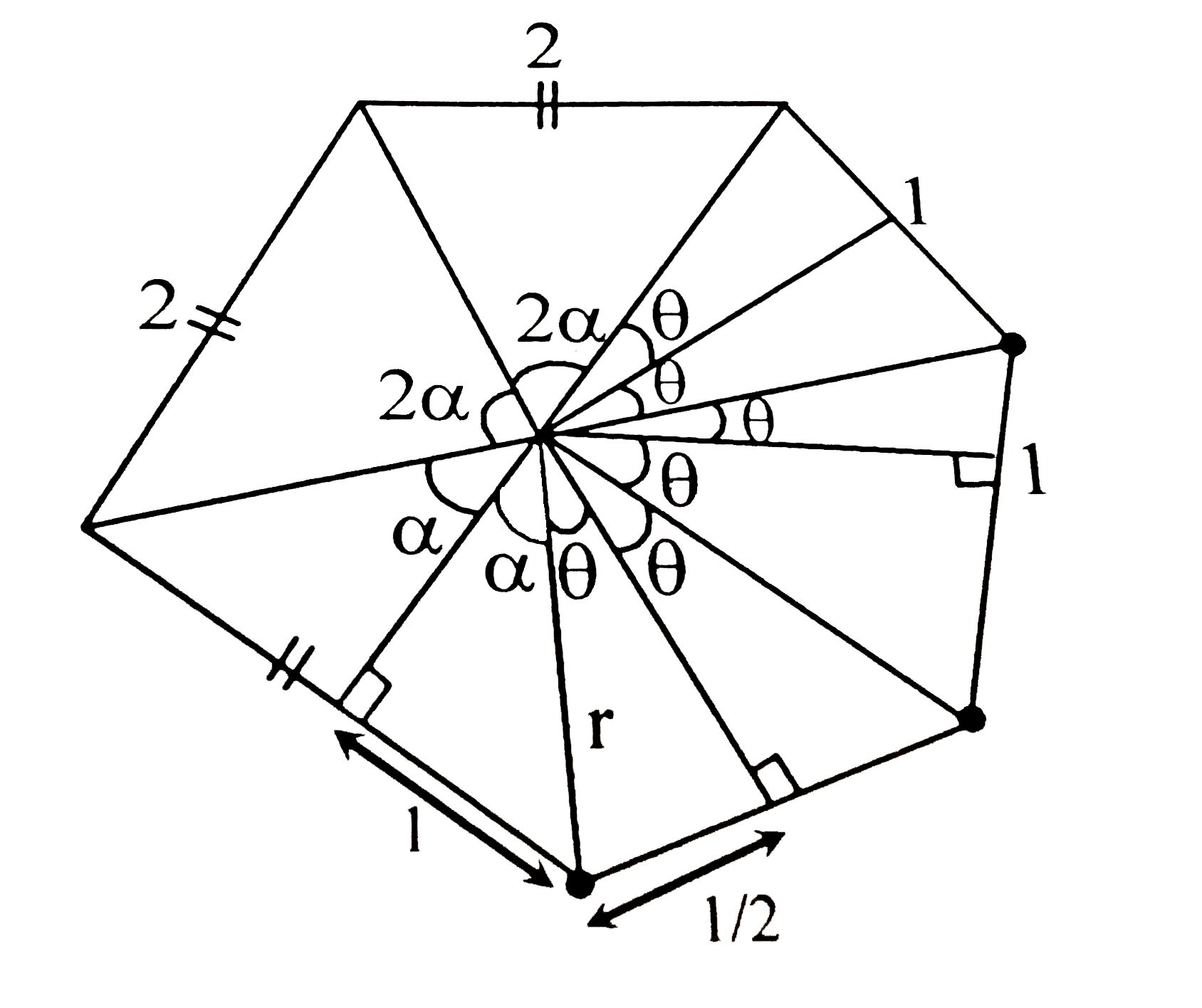
- Suppose ABCDEF is a hexagon such that AB=BC=CD=1 and DE=EF=FA=2. If th...
Text Solution
|
- If a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+F...
Text Solution
|
- Suppose ABCDEF is a hexagon such that AB=BC=CD=1 and DE=EF=FA=2. If th...
Text Solution
|
- In a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+F...
Text Solution
|
- एक षटभुज ABCDEF एक वृत्त के परिगत बनाया गया है, तो सिद्ध कीजिए कि A...
Text Solution
|
- In DeltaABC and DeltaDEF, AB= DE, AB abs DE, BC= EF and BC abs EF. Ver...
Text Solution
|
- In DeltaABC and DeltaDEF, AB= DE, AB abs DE, BC= EF and BC abs EF. Ver...
Text Solution
|
- In DeltaABC and DeltaDEF, AB= DE, AB abs DE, BC= EF and BC abs EF. Ver...
Text Solution
|
- In DeltaABC and DeltaDEF, AB= DE, AB abs DE, BC= EF and BC abs EF. Ver...
Text Solution
|