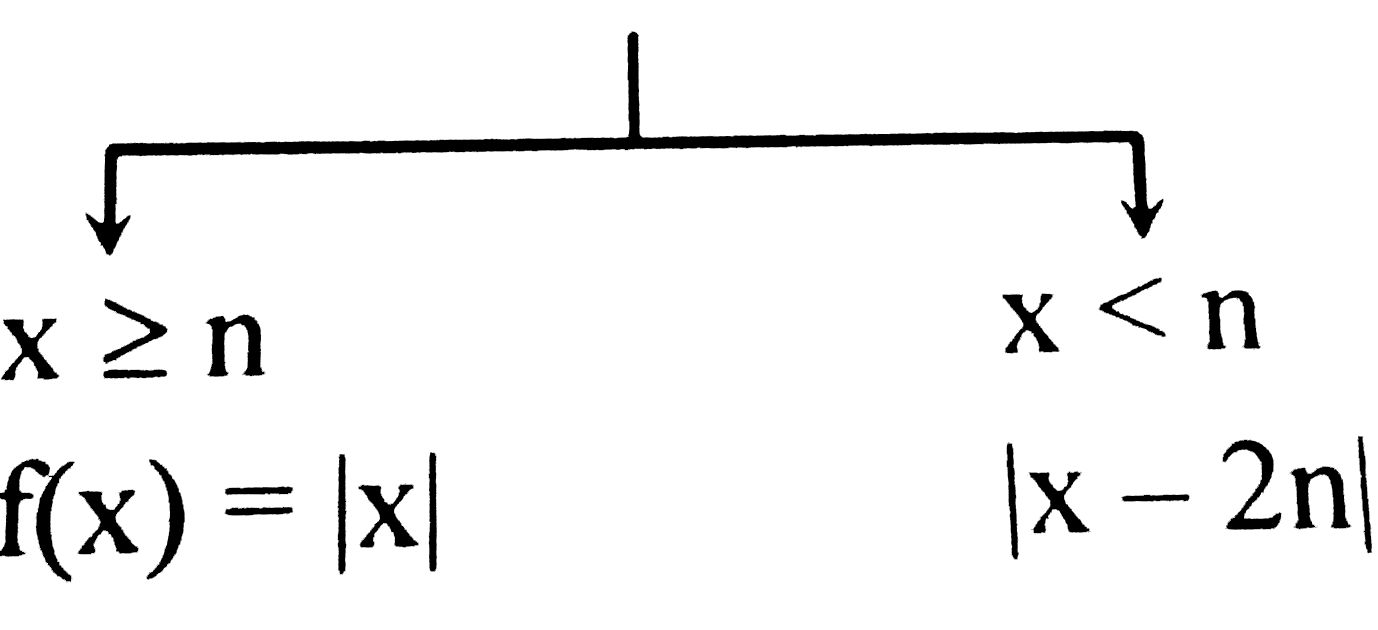
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Define a function f : R to R by f(x)=max {|x|,|x-1|, . . .|x-n|} ...
Text Solution
|
- Define a function f:R rarr R by f(x)=max{|x|,|x-1|,...|x-2n|} where n ...
Text Solution
|
- एक फलन f: R rarr R इस प्रकार परिभाषित है f(x)=max {x, x^(3)}. तब उन सभ...
Text Solution
|
- Let f : R - {n} rarr R be a function defined by f(x)=(x-m)/(x-n), wher...
Text Solution
|
- माना कि फलन f : N to N इस प्रकार परिभाषित है :f(x) =2x, जहाँ x in N ...
Text Solution
|
- If f (x) is a function such that f(x+y)=f(x)+f(y) and f(1)=7" then ...
Text Solution
|
- Let f be a function defined on R by f(x)=lim(n to oo) (log (3+x)-x^(2n...
Text Solution
|
- Let f: R rarr R be defined by f(x)=|x-2n| if x in [2 n -1, 2n+1], (n i...
Text Solution
|
- f(x)>0AAx in R and is bounded. If lim(n->oo)[int0^a(f(x)dx)/(f(x)+f(a...
Text Solution
|