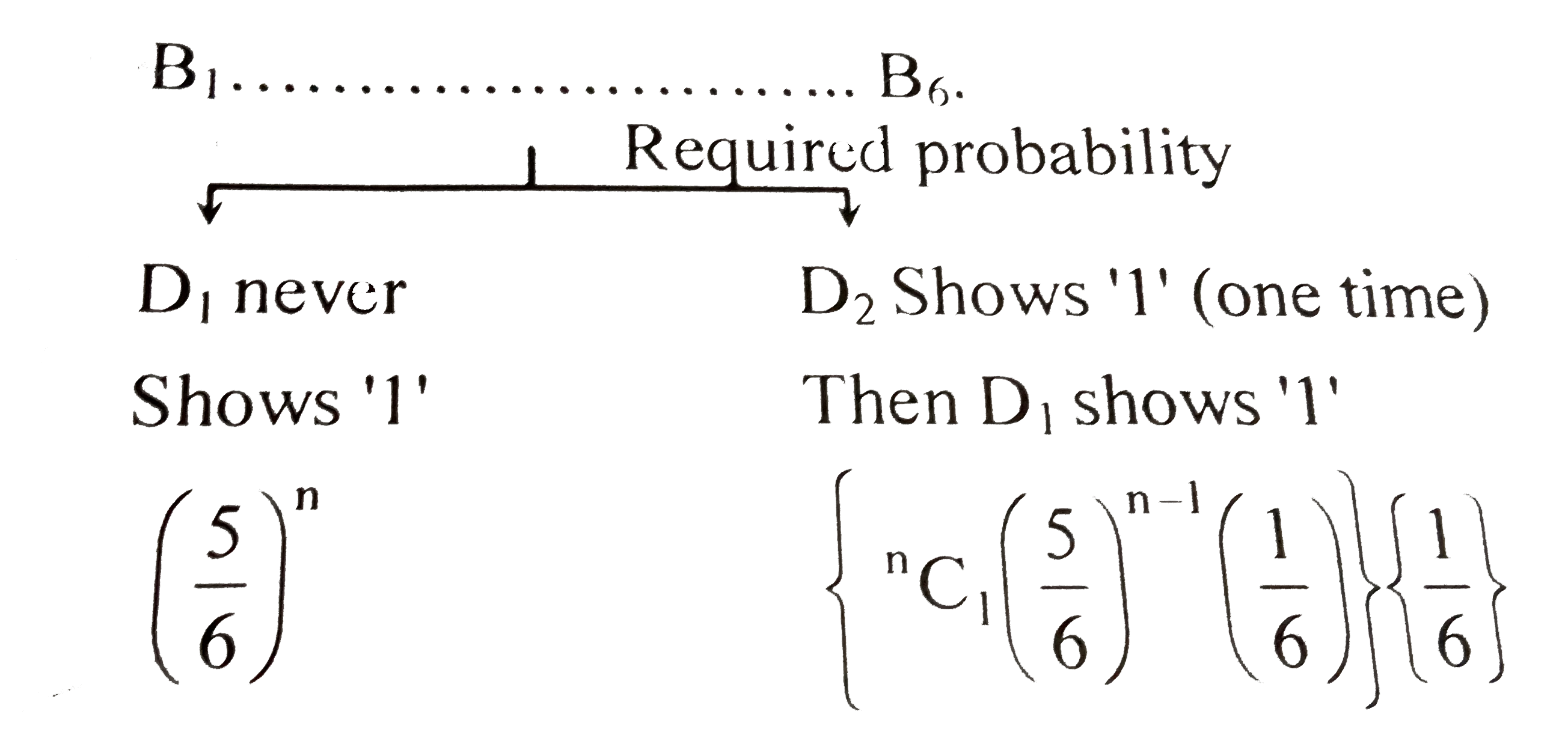A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- There are boxes labelled B(1),B(2), . . . .,B(6). In each trial, two f...
Text Solution
|
- For k=1,2,3 the box Bk contains k red balls and (k+1) white balls. Let...
Text Solution
|
- There are boxes labelled B(1),B(2), . . . .,B(6). In each trial, two f...
Text Solution
|
- Let A(n) = a(1) + a(2) + "……" + a(n), B(n) = b(1) + b(2) + b(3) + "…."...
Text Solution
|
- A box B(1) contains 1 white ball, 3 red balls, and 2 black balls. An- ...
Text Solution
|
- A box B(1) contains 1 white ball 3 red balls and 2 black balls. Anothe...
Text Solution
|
- A box B(1) contains 1 white ball 3 red balls and 2 black balls. Anothe...
Text Solution
|
- If a=a(1)i+a(2)j+a(3)k, b=b(1)i+b(2)j+b(3)k, c=c(1)i+c(2)j+c(3)k, d=d(...
Text Solution
|
- A box B(1) contains 1 white ball, 3 red balls, and 2 black balls. An- ...
Text Solution
|