Home
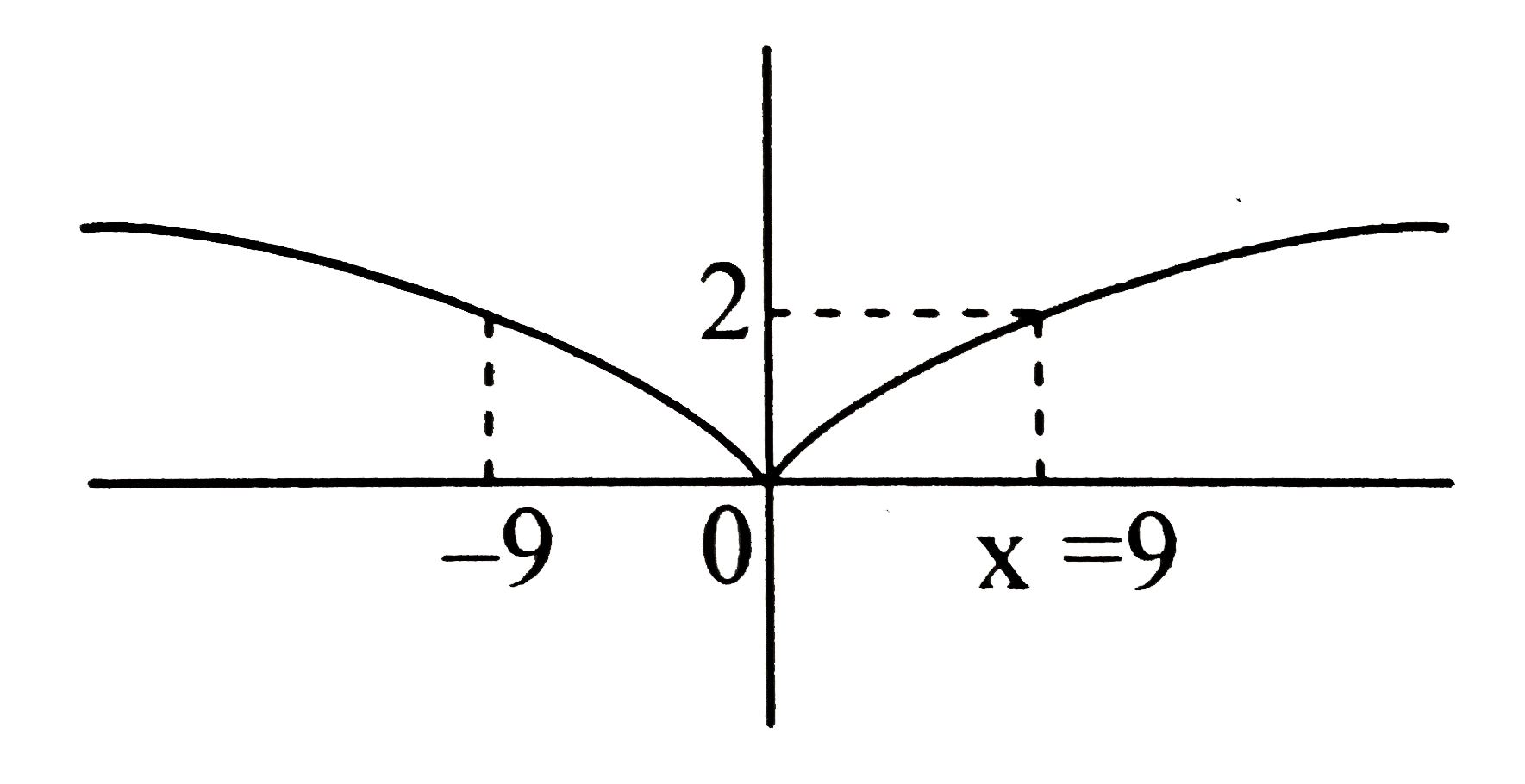
Class 12
MATHS
Let R be the set of real number and f: R...

Let R be the set of real number and `f: R to R` be given by `f(x)=sqrt(|x|)- log (1+|x|)`. We now make the following assertions :
I. There exists a real number A such that `f(x) leA` for all x.
II. There exists a real number B such that `f(x) geB` for all x.

A

I is true and II is false

B

I is false and II is true

C

I and II both are true

D

I and II both are false

Text Solution

Verified by Experts

The correct Answer is:
B
graph of given function actually look like this

Clear from graph option (B) is right.
Promotional Banner

Topper's Solved these Questions

  • KVPY

    KVPY PREVIOUS YEAR|Exercise PART-1 MATHEMATICS|20 Videos

  • KVPY

    KVPY PREVIOUS YEAR|Exercise PART-2 MATHMATICS|10 Videos

  • KVPY

    KVPY PREVIOUS YEAR|Exercise Part A - Mathematics|20 Videos

  • KVPY 2021

    KVPY PREVIOUS YEAR|Exercise PART II MATHEMATICS|4 Videos

Similar Questions

Explore conceptually related problems

Let R be the set of real numbers and f:R rarr R be given by,f(x)=x^(2)+2. Find f^(-1){11,16}

R is the set of real numbers,If f:R rarr R is defined by f(x)=sqrt(x) then f is

Let R be the set of all real numbers and f : R rarr R be given by f(x) = 3x^(2) + 1 . Then the set f^(-1) ([1, 6]) is

Let R be the set of real numbers and let f:RtoR be a function such that f(x)=(x^(2))/(1+x^(2)) . What is the range of f?

Let R be the set of all real numbers. The function f:Rrarr R defined by f(x)=x^(3)-3x^(2)+6x-5 is

Let R be the set of all real numbers let f: R to R : f(x) = sin x and g : R to R : g (x) =x^(2) . Prove that g o f ne f o g

Let R be the set of real numbers and f : R to R be such that for all x and y in R, f(x) -f(y)|^(2) le (x-y)^(3) . Prove that f(x) is a constant.

Let R be the set of real number and the mapping f :R to R and g : R to R be defined by f (x)=5-x^(2)and g (x)=3x-4, then the value of (fog) (-1) is