Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTANTICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE) LEVEL - I|14 VideosELECTROSTANTICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS (SUBJECTIVE) FILL IN THE BLANKS|4 VideosELECTROSTANTICS
FIITJEE|Exercise SOLVED PROBLEMS (OBJECTIVE)|15 VideosELECTROMAGNETIC WAVE & WAVE OPTICS
FIITJEE|Exercise ASSIGNMENT PROBLEMS Objective : Level-II (MULTI CHOICE SINGLE CORRECT)|21 VideosELECTROSTATICS
FIITJEE|Exercise Example|14 Videos
Similar Questions
Explore conceptually related problems
FIITJEE-ELECTROSTANTICS-EXERCISE
- What is the electric field intensity at any point on the axis of a cha...
Text Solution
|
- Point charges +q and -q are kept alternately at the corners of a cube ...
Text Solution
|
- A particle of mass 100 gm and charge 2muC is released from a distance ...
Text Solution
|
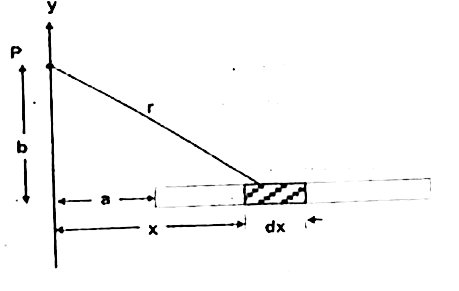
- Calculate the potential due to a thin charged rod of length L at the p...
Text Solution
|
- Electric field in a region is given by E=(2hati+3hatj-4hatk)V//m. Find...
Text Solution
|
- A dipole of dipole moment vecp is kept along an electric field E such ...
Text Solution
|
- Two metal spheres of radius r have centers at a distance d apart in ai...
Text Solution
|
- Find the equivalent capacitance between points A and B. Capacitance of...
Text Solution
|
- Two concentric shells of radii R and 2R are shown in the figure. Initi...
Text Solution
|
- In the figure shown a parallel plate capacitor is connected across a s...
Text Solution
|