Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CPC CAMBRIDGE PUBLICATION-TRIANGLES-Exercise 2.6 (Optional)
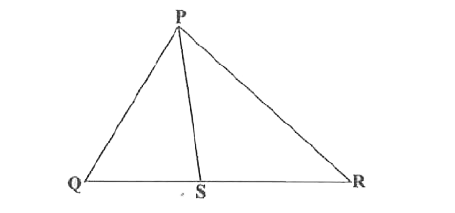
- In Fig . PS is the bisecto of angle QPR of Delta PQR . Prove that ...
Text Solution
|
- In Fig. D is point on hypotenuse AC of Delta ABC , BD bot AC DM bot B...
Text Solution
|
- In Fig , ABC is a triangle in which angleABCgt90^(@) and AD bot CB, ...
Text Solution
|
- In Fig . ABC is a triangle in which angleABClt90^(@)and AD botBC. P...
Text Solution
|
- In Fig . AD is a median of a triangle ABD and AM bot BC. Prove that...
Text Solution
|
- Prove that sum of the squares of the side of a rhombus is equal to th...
Text Solution
|
- In Fig . two chords AB and CD intersect each other at the point P. pro...
Text Solution
|
- In Fig. two chords AB and CD of a circle intersect each other at the p...
Text Solution
|