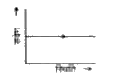
हर प्रकार की गतिकीय समस्याओं के विश्लेषण के लिए फेज समष्टि चित्रम ( Phase space diagrams ) का उपयोग किया जाता है। प्रारंभिक दशा, स्थिति व् सवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझाने में बहुत उपयोगी है। यहाँ हम एक विमीय सरल गतिकीय निकायों की बात करते है । इनके संवेग Y - अक्ष पर रखते है। तब फेज समष्टि चित्राम इस समतल में एक `x(t) vs. p(t) ` (i ) वक्र होता। वक्र पर तीर समय बढ़ाने की दिशा दर्शाता है। उदाहरण के लिए, स्थिर वेग से चल रहें कण के लिए फेज समष्टि चित्राम सरल रेखा है जिसे चित्र में दिखाया गया है। चिन्ह परिपाटी में स्थित या संवेग को ऊपर (या दाहिने ) और धनात्मक तथा निचे (या बायीं) और ऋणात्मक मान जाता है

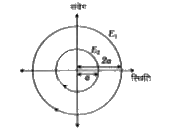
सरल आवर्त दोलन (SHM ) का फेज समष्टि चित्राम उदगम पर केंद्रित वृत है। चित्र में दर्शया गए दो वृत, एक ही दोलक के लिए है, जब उसकी आरंभिक अवस्थाएं भिन्न है ,तथा `E_1` व् `E_2` क्रमशः दोलक की कुल यांत्रिक ऊर्जाएं है। तब

Options

A. `E_(1)=sqrt2 E_(2)`
B. `E_(1)=2 E_(2)`
C. `E_(1)=4 E_(2)`
D. `E_(1)=16 E_(2)`

Answer

C

Explanation

सरल आवृत गाती में प्रथम स्थिति में दोलक (Oscillator) का आयाम =2a द्वितीय स्थिति में दोलक आयाम =a
कुल ऊर्जा `E=1/2 m omega^(2).A ^(2)`
या `E alpha A^(2)`
`therefore E_(2)/E_(1)=((A_(2))/A_(1))^(2)`
`E_(2)/E_(1)=((a)^(2))/((2a)^(2))" या "E_(1)=4 E_(2)`