Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
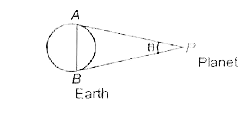
- The parallax of a heavenly body measured from tow points diametrically...
Text Solution
|
- The parallax of a heavenly body measured from tow points diametrically...
Text Solution
|
- Assertion :- The mechanical energy of earth-moon system remains same w...
Text Solution
|
- The parallex of a heavenly body measured ffrom two points diametricall...
Text Solution
|
- Compare the weight of a body 100 km above and 100 km below the surface...
Text Solution
|
- पृथ्वी पर दो व्यासतः विपरीत स्थित बिंदुओं से एक खगोलीय पिंड क...
Text Solution
|
- To view heavenly objects like stars, is used
Text Solution
|
- पृथ्वी के व्यास के सिरों के बिंदुओं से किसी आकाशीय पिंड का लंबन कोण 2...
Text Solution
|
- पृथ्वी की दो व्यासतः अभिमुख (Diametrically opposite ) बिंदुओं से किसी...
Text Solution
|