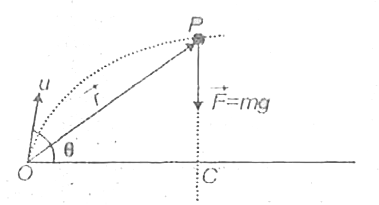
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m is projected with velocity v at an angle theta w...
Text Solution
|
- A particle of mass m is thrown with speed v(0) at angle 30^(@) with ho...
Text Solution
|
- A particle of mass m is projected with a velocity mu at an angle of th...
Text Solution
|
- A particle of mass m is projected with velocity v at an angle theta wi...
Text Solution
|
- A particle of mass m is projected at an angle of 45^(@) with the horiz...
Text Solution
|
- A particle is projected fro the ground with an initial speed v at an a...
Text Solution
|
- m द्रव्यमान का एक कण वेग से क्षैतिज से theta कोण पर फेंका जाता है। जब...
Text Solution
|
- A particle is projected from the ground with an initial speed v at an ...
Text Solution
|
- A particle is projected from the ground with an initial speed of v at ...
Text Solution
|