लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
विद्युत क्षेत्र
SCIENCE PUBLICATION|Exercise अतिलघूत्तरात्मक प्रश्न|55 Videosविद्युत क्षेत्र
SCIENCE PUBLICATION|Exercise पाठ्यपुस्तक के प्रश्न- उत्तर (वस्तुनिष्ठ प्रश्न )|15 Videosविद्युत -चुम्बकीय तरंगे , संचार एवं समकालीन भौतिकी
SCIENCE PUBLICATION|Exercise अन्य महत्वपूर्ण प्रश्न ( आंकिक प्रश्न )|5 Videosविद्युत चुम्बकीय प्रेरण
SCIENCE PUBLICATION|Exercise अन्य महत्वपूर्ण प्रश्न ( आंकिक प्रश्न )|11 Videos
SCIENCE PUBLICATION-विद्युत क्षेत्र -अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न )
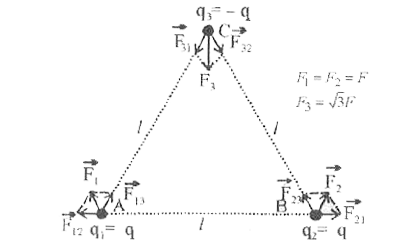
- चित्र में दर्शाए अनुसार किसी समबाहु त्रिभुज के शीर्षों पर स्थित आवेशों...
Text Solution
|
- दो समान आवेश d दूरी पर स्थित हैं एक तीसरे आवेश को लम्बार्धक पर x दूरी ...
Text Solution
|
- ABC एक समकोण त्रिभुज है, जिसमें AB = 3cm, BC = 4cm एवं angleABC =pi...
Text Solution
|
- दो बिन्दु आवेश Q व -3Q एक दूसरे से कुछ दूरी पर रखे हैं। यदि Q स्थिति प...
Text Solution
|
- मूल बिन्दु O पर X-अक्ष के अनुदिश एक वैद्युत द्विध्रुव रखा गया है । इस ...
Text Solution
|