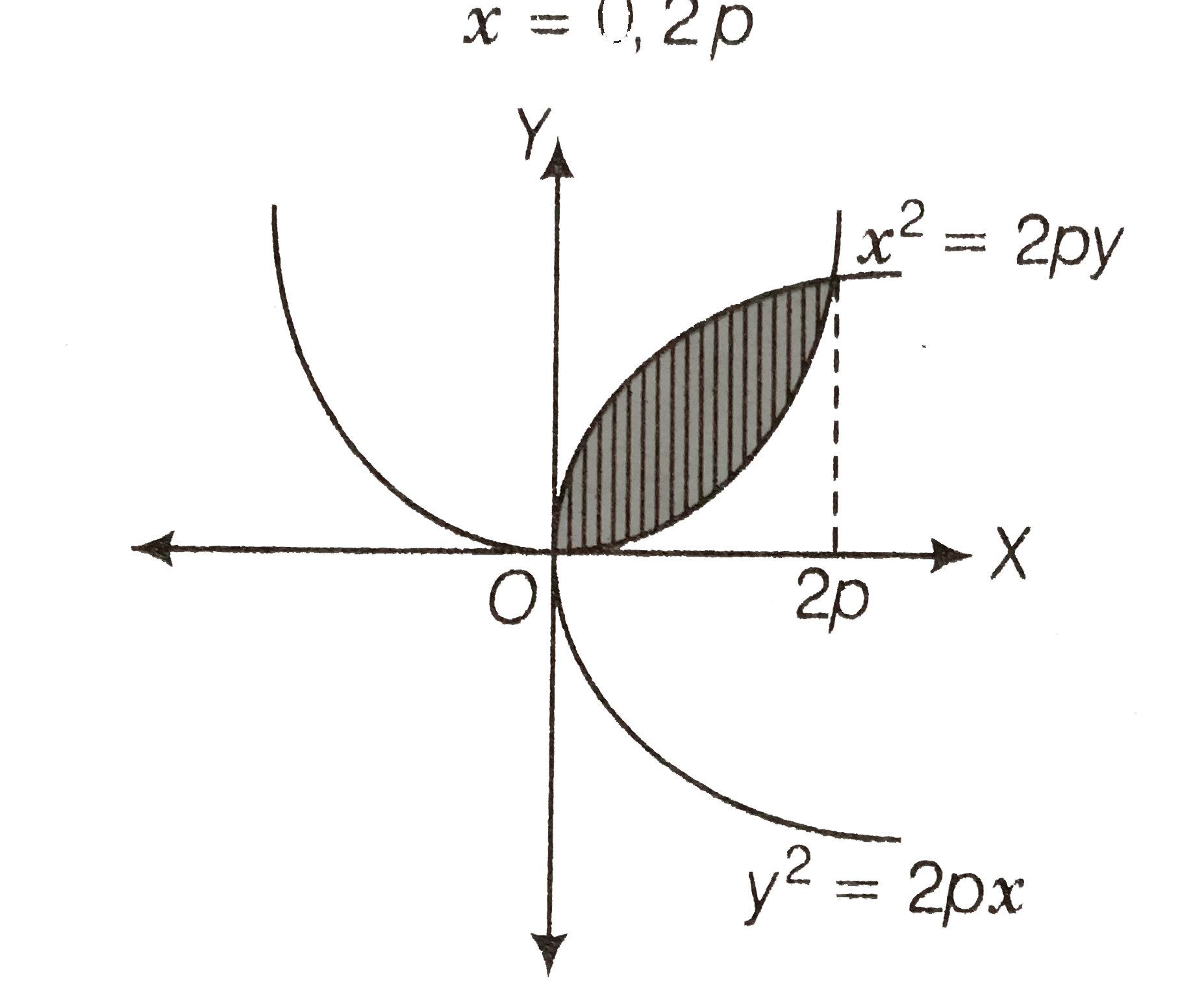A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT EXEMPLAR-APPLICATION OF INTEGRALS-Application Of Integrals
- Find the area of the region bounded by the curve y^(2)=9x" and " y=3x.
Text Solution
|
- Find the area of the region bounded by the parabola y^(2)=2px and x^(2...
Text Solution
|
- Find the area of the region bounded by the curve y=x^(3),y=x+6" and "x...
Text Solution
|
- Find the area of the region bounded by the curve y^(2)=4x" and " x^(2)...
Text Solution
|
- Find the area of the region included between y^(2)=9x" and "y=x.
Text Solution
|
- Find the area of the region enclosed by the parabola x^(2)=y and the l...
Text Solution
|
- Find the area of the region bounded by line x = 2 and parabola y^(2)=8...
Text Solution
|
- Sketch the region {(x, 0):y=sqrt(4-x^(2))} and X-axis. Find the area o...
Text Solution
|
- Calculate the area under the curve y=2sqrtx included between the lines...
Text Solution
|
- Using integration, find the area of the region bounded by the line 2y=...
Text Solution
|
- Draw a rough sketch of the curve y=sqrtx-1) in the interval [1, 5]. Fi...
Text Solution
|
- Determine the area under the curve y=sqrt(a^(2)-x^(2)) included betwee...
Text Solution
|
- Find the area if the region bounded by y=sqrtx" and " y=x.
Text Solution
|
- Find the area enclosed by the curve y=-x^(2) and the straight line x+y...
Text Solution
|
- Find the area bounded by the curve y=sqrtx,x=2y+3 in the first quadran...
Text Solution
|
- Find the area of the region bounded by the curve y^(2)=2x" and "x^(2)+...
Text Solution
|
- Find the area of region by the curve y=sinx" between "x=0" and "x=2pi.
Text Solution
|
- Using integration, find the area of the triangle ABC whose vertices ar...
Text Solution
|
- Find the area of the region {(x, y) : y^2 <=6ax and x^2+y^2<=16a^2} ...
Text Solution
|
- Compute the area bounded by the lines x +2y=2,y-x=1" and " 2x+y=7.
Text Solution
|