Home
Class 11
PHYSICS
A bob of mass m, suspended by a string o...

A bob of mass m, suspended by a string of length `l_1` is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length `l_2`, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio `(l_1)/(l_2)` is

A

1

B

3

C

5

D

`1//5`

Text Solution

Verified by Experts

The correct Answer is:
C
Velocity of the first bob at A = `sqrt(5gl_1)`
Velocity of the first bob at B=`sqrt(gl_1)`
At point B it collides elastically with another bob of same mass m suspended by a string of length `l_2` as shown in figure.
When two bodies of equal masses undergoes an elastic collision, their velocities are interchanged.
`therefore` Velocity of the second bob at B=`sqrt(gl_1)`
But to complete the vertical circle, the velocity of the second bob at B = `sqrt(5gl_2)`
`therefore sqrt(gl_1)=sqrt(5gl_2) " " or " " l_1/l_2=5`
Promotional Banner

Topper's Solved these Questions

  • WORK , ENERGY AND POWER

    NCERT FINGERTIPS|Exercise NCERT Exemplar|18 Videos

  • WORK , ENERGY AND POWER

    NCERT FINGERTIPS|Exercise Assertion And Reason|15 Videos

  • WORK , ENERGY AND POWER

    NCERT FINGERTIPS|Exercise Collisions|15 Videos

  • WAVES

    NCERT FINGERTIPS|Exercise Assertion And Reason|15 Videos

Similar Questions

Explore conceptually related problems

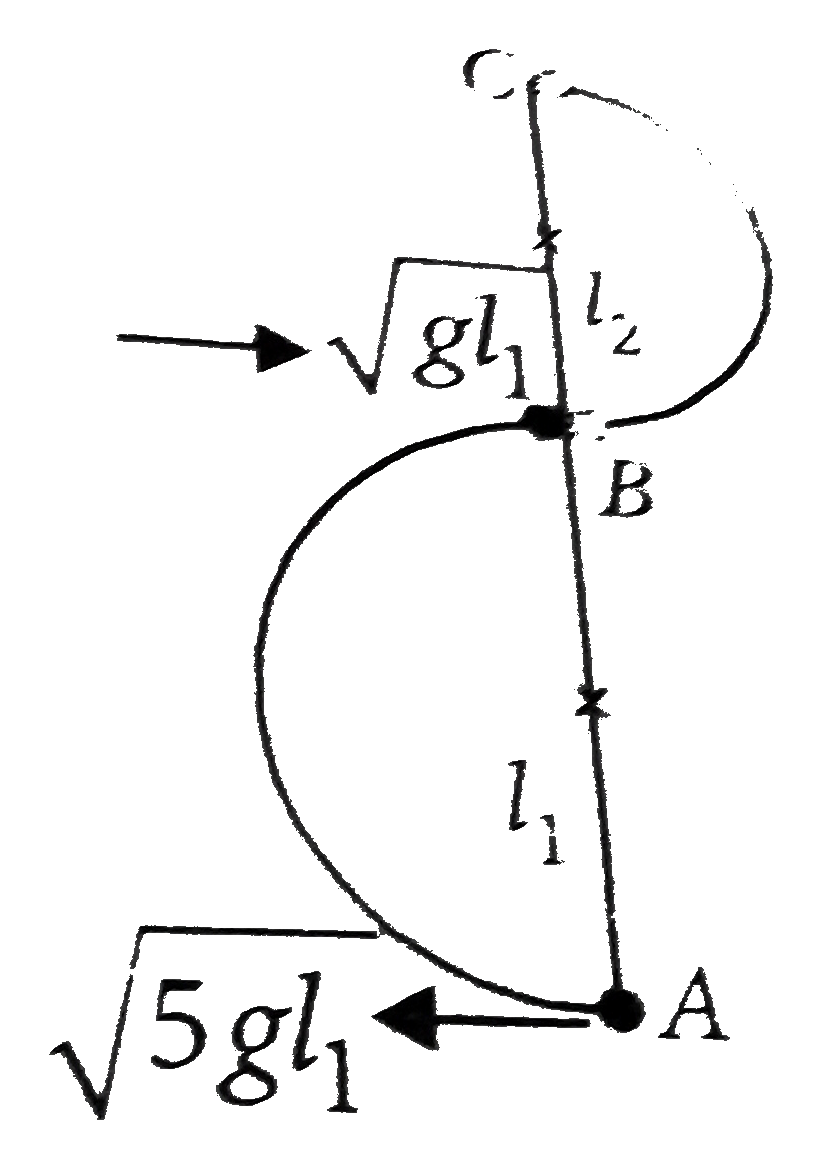
A particle of mass m suspended by a string of length l revolves in a horizontal circle ( theta is the angle the string makes with vertical). Which of the following statement(s) is // are correct?

A body of mass m is suspended from a string of length l. What is minimum horizontal velocity that should be given to the body in its highest position so that it may complete one full revolution in the vertical plane with the point of suspension as the centre of the circle.

A body of mass m is suspended from a string of length l . What is minimum horizontal velocity that should be given to the body in its lowest position so that it may complete one full revolution in the vertical plane with the point of suspension as the centre of the circle

A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at (a) Point B ? (b) Point C? (c) Point X?

A bob of mas M is suspended by a massless string of length L . The horizontal velocity v at position A is just sufficient to make it reach the point B . The angle theta at which the speed of the bob is half of that at A , satisfies. .

A bullet ofmass m is fired with a velocity 10m//s at angle theta with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2//5m and gets embedded in the bob. After th collision the string moves through an angle of 60^(@) . The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet is

A bob of mass ‘m’ is suspended by a light string of length ‘L’. It is imparted a minimum horizontal velocity at the lowest point A such that it just completes half circle reaching the top most position B. The ratio of kinetic energies frac{(K.E.)_A}{(K.E)_B} is