Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS-GRAVITATION-NCERT Exemplar
- The earth is an approximate sphere. If the interior contained matter w...
Text Solution
|
- As observed from the earth, the sun appears to move an approx. circula...
Text Solution
|
- Different points in the earth are at slightly different distance from ...
Text Solution
|
- Satellites orbiting the earth have finite life and sometimes debris of...
Text Solution
|
- Both earth and moon are subjected to the gravitational force of the su...
Text Solution
|
- In our solar system, the inter-planetery region has chunks of matter (...
Text Solution
|
- Choose the wrong option.
Text Solution
|
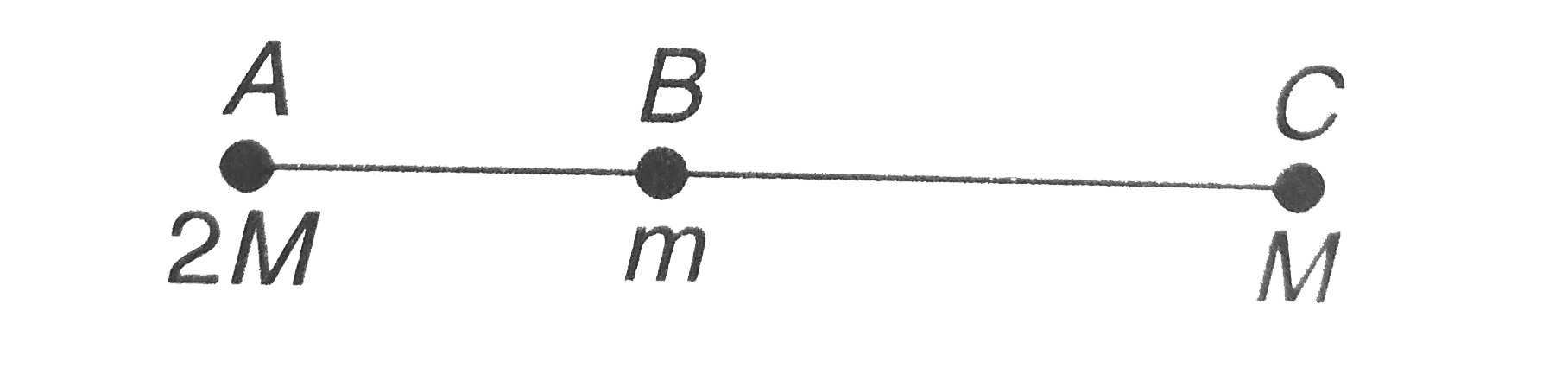
- particles of masses 2M m and M are resectively at points A , B and C w...
Text Solution
|