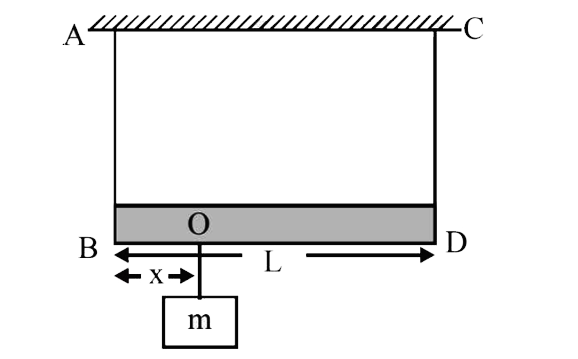
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
WAVES
NCERT FINGERTIPS|Exercise NCERT Exemplar|10 VideosWAVES
NCERT FINGERTIPS|Exercise Assertion And Reason|15 VideosWAVES
NCERT FINGERTIPS|Exercise Doppler Effect|10 VideosUNITS AND MEASUREMENTS
NCERT FINGERTIPS|Exercise Assertion And Reason|15 VideosWORK , ENERGY AND POWER
NCERT FINGERTIPS|Exercise Assertion And Reason|15 Videos
Similar Questions
Explore conceptually related problems
NCERT FINGERTIPS-WAVES-Higher Order Thinking Skills
- One end of a taut string of length 3m along the x-axis is fixed at x =...
Text Solution
|
- Vibrating tuning fork of frequency n is placed near the open end of a ...
Text Solution
|
- Three travelling waves are superimposed. The equations of the wave are...
Text Solution
|
- Find the temperature at which the fundamental frequency of an organ pi...
Text Solution
|
- An organ pipe of cross-sectional area 100 cm^(2) resonates with a tuni...
Text Solution
|
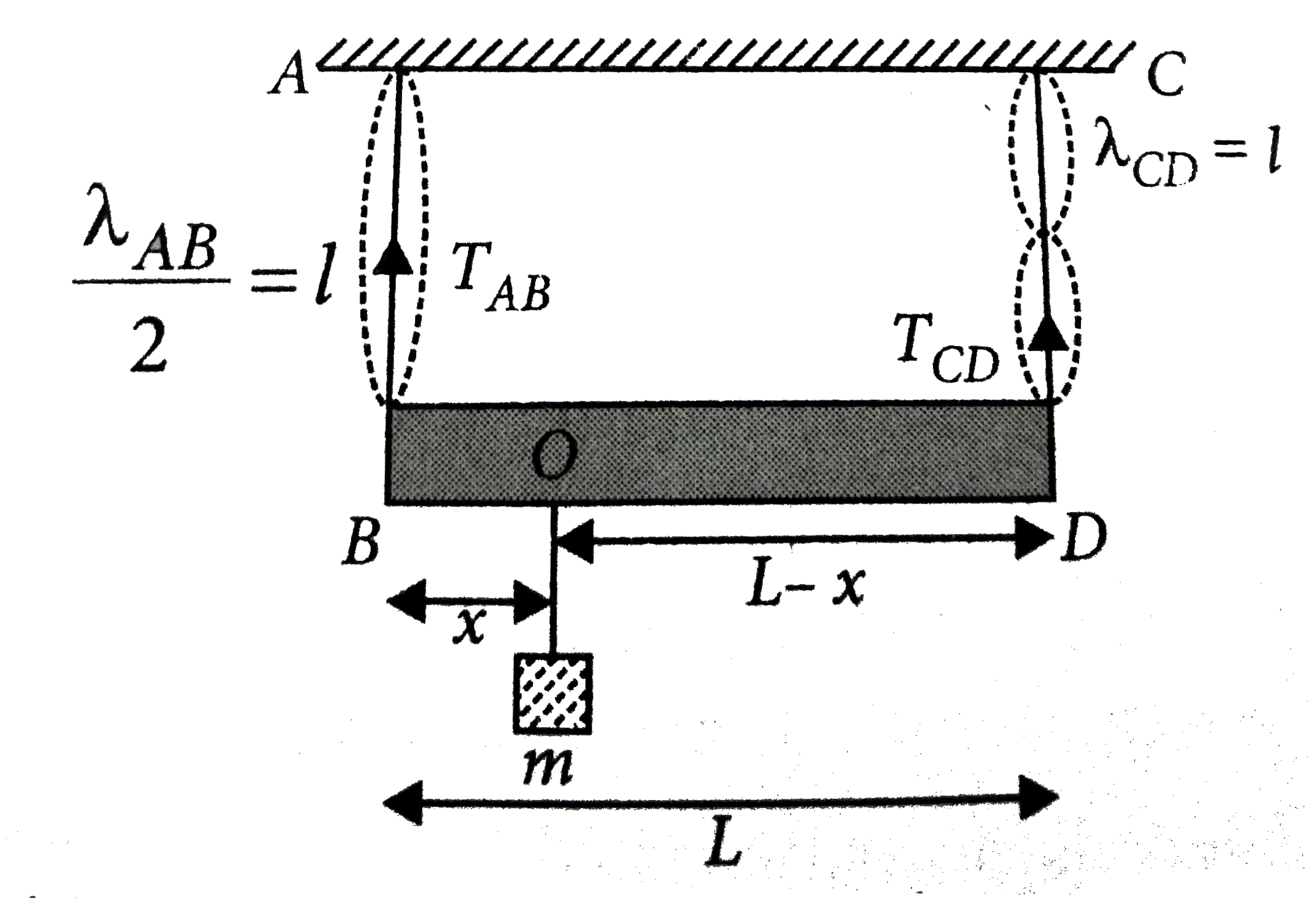
- A massless rod of length L is suspended by two identical string AB and...
Text Solution
|
- A stationary source is emitting sound at a fixed frequency f(0), which...
Text Solution
|
- Two pulses in a stretched string whose centres are initially 8 cm apar...
Text Solution
|