Home
Class 9
MATHS
In a quadrilateral ABCD, AO and BO are t...

In a quadrilateral ABCD, AO and BO are the bisectors of `angleA and angleB` respectively. Prove that `angleAOB=1/2(angleC+angleD).`

Text Solution

Verified by Experts

In`DeltaDeltaOB+angle1+angle2=180^(@)`
`implies" "angleAOB=180^(@)-(angle1+angle2)`
`implies" "angleAOB=180^(@)-((angleA)/(2)+(angleB)/(2))`
`implies" "angleAOB=180^(@)-1/2[360^(@)-(angleC+angleD)](because angleA+angleB+angleC +angleD=360^(@))`
`implies" "angleAOB=180^(@)-180^(@)+1/2(angleC+angleD)`
`implies" "angleAOB=1/2(angleC+angleD)`
Promotional Banner

Topper's Solved these Questions

  • QUADRILATERALS

    NAGEEN PRAKASHAN|Exercise Problems From NCERT/exemplar|11 Videos

  • QUADRILATERALS

    NAGEEN PRAKASHAN|Exercise Exercise 8a|29 Videos

  • PROBABILITY

    NAGEEN PRAKASHAN|Exercise Revision Exercise (very Short Answer /short Answer Questions)|10 Videos

  • STATISTICS

    NAGEEN PRAKASHAN|Exercise Revision Exercise|10 Videos

Similar Questions

Explore conceptually related problems

In a quadrilateral ABCD,AO and BO are the bisectors of A/_ and /_B respectively. Prove that /_AOB=(1)/(2)(/_C+/_D)

In quadrilateral ABCD,AO and BO are the bisectors of /_A and /_B respectively.Prove that /_AOB=(1)/(2)(/_C+/_D)

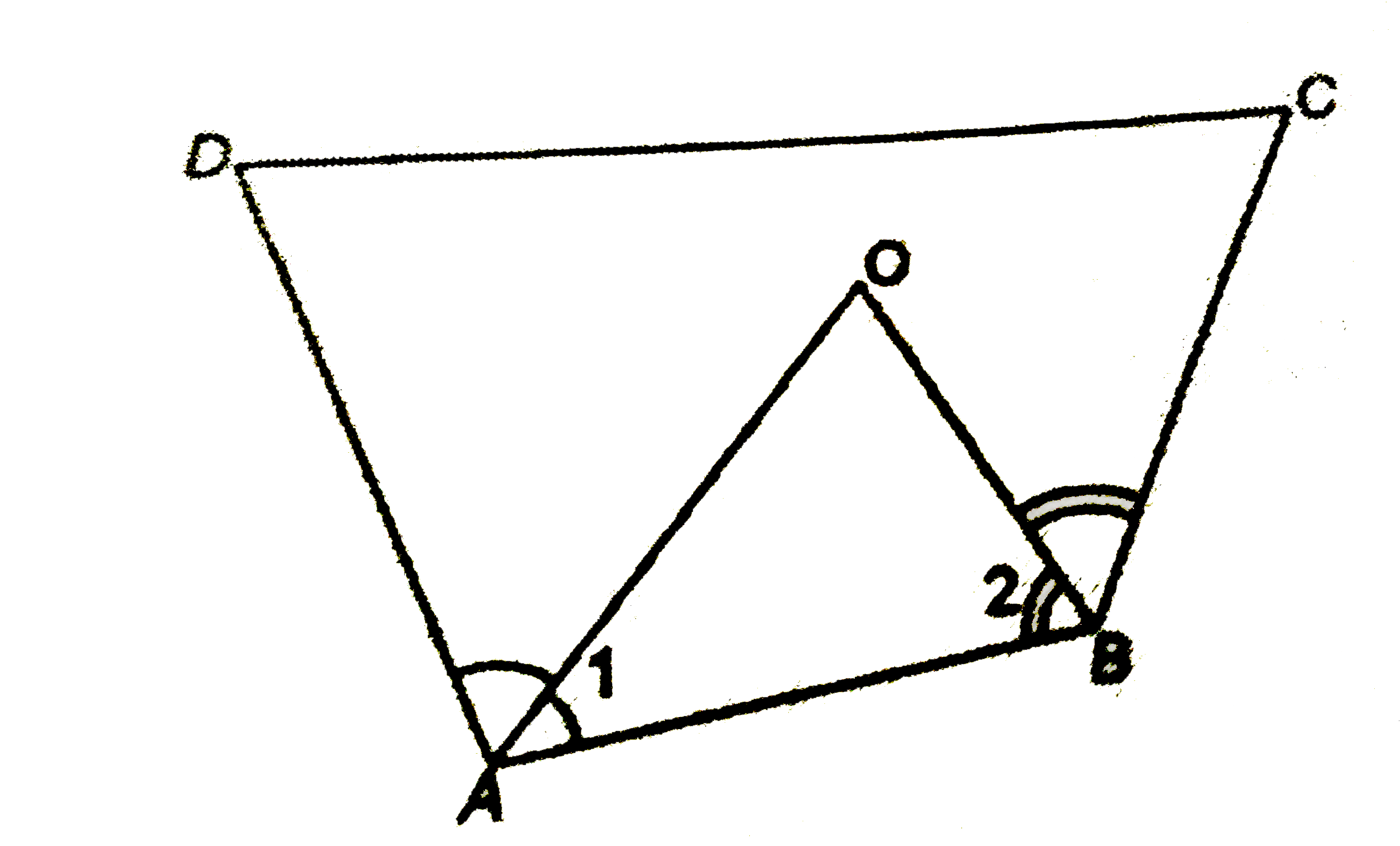
In a quadrilateral ABCD, AO and BO are the bisectors of angle A and angle B respectively, angle C = 70^(@) and angle D=30^(@). " Then, " angle AOB= ?

In the adjoining figure, ABCD is a parallelogram , AO and BO are the bisectors of angleA and angleB respectively. Prove that angleAOB=90^@ .

In a quadrilateral ABCD, CO and DO are the bisectors of /_C and /_D respectively. Prove that /_COD=(1)/(2)(/_A+/_B)

In a quadrilateral ABCD,CO and DO are the bisectors of /_C and /_D respectively. Prove that /_COD=(1)/(2)(/_A+/_B)

In the given figure, ABgtAC. If BO and CO are the bisectors of angleB and angleC respectively then

In a quadrilateral ABCD, OA and OB are the angle bisectors of angleDAB" and " angleCBA . If angleADC=70^(@)" and "angleBCD=80^(@) then find angleAOB ?

In a triangle ABC , OB and OC are the bisector of angle angleB and angleC respectively . angleBAC = 60^@ . The angle angleBOC will be :

In a quadrilateral ABCD the linesegment bisecting angleC and angleD meet at E. Prove that angleA+angleB=2angleCED.