A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-HERONS'S FORMULA-Revision Exercise
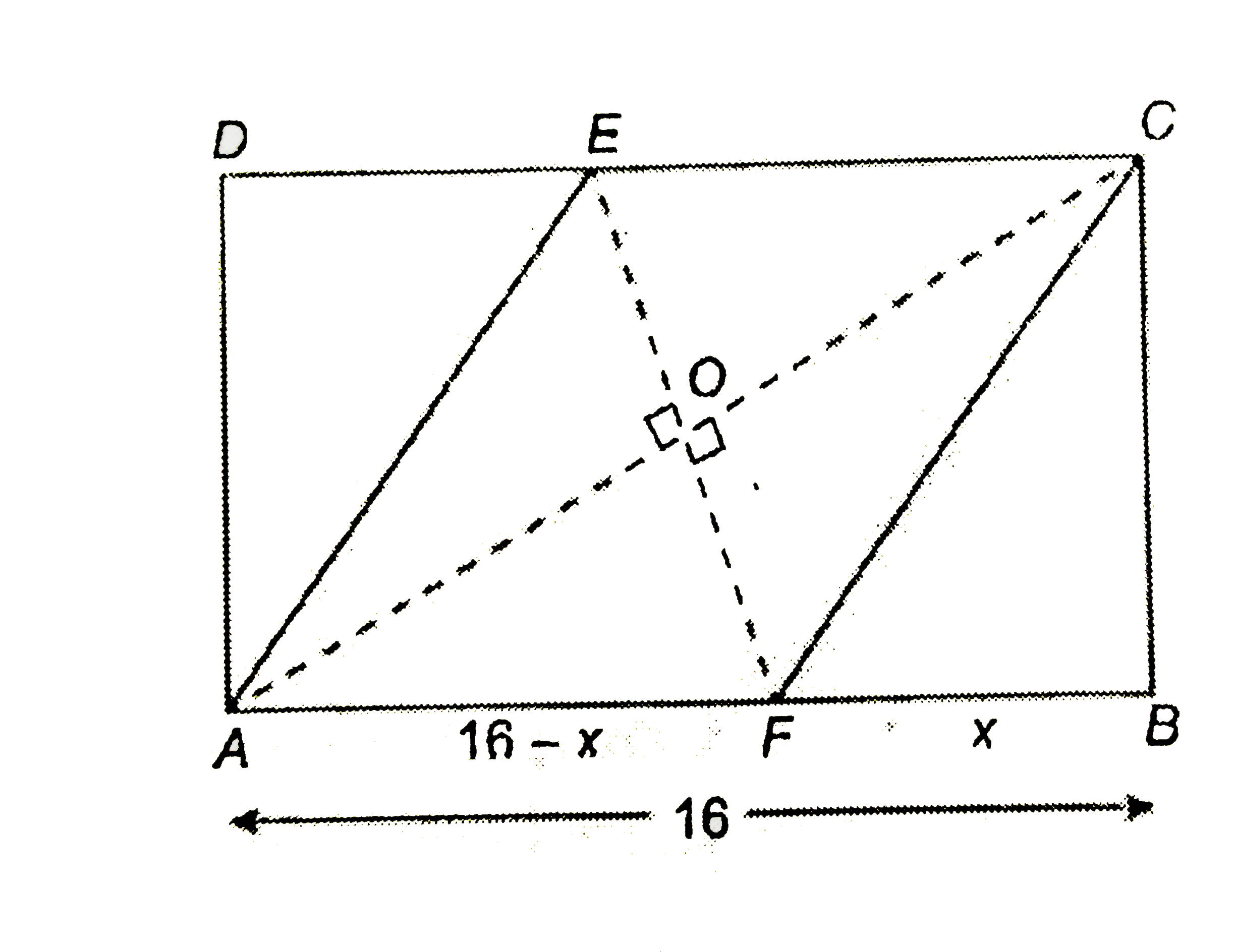
- ABCD is a rectangle with AB=16 units and BC=12 units. F is a point on ...
Text Solution
|
- The lengths of the three sides of a Delta are 3, 4 and 5 cm, respectiv...
Text Solution
|
- Each side of an equilateral triangle measure 10 cm. Find the area of ...
Text Solution
|
- The base of an isosceles triangle is 16 cm. If both the equal sides be...
Text Solution
|
- The sides of a triangle are in the ratio 5 : 12 : 13 and its perimeter...
Text Solution
|
- Calculate the area of an equilateral triangle whose height is 20 cm.
Text Solution
|
- Find the area of triangle whose sides are 17 cm, 8 cm and 15 cm. Also ...
Text Solution
|
- Find the area of the trapezium given in adjoining figure.
Text Solution
|
- A park is in the shape of quadrilateral ABCD in which AB = 9 cm, BC =...
Text Solution
|
- Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm ...
Text Solution
|
- Find the area of the trapezium given in given figure.
Text Solution
|
- Find the area of the given figure Given AB = 18 cm, BC = 7 cm, CD = ...
Text Solution
|