Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-SETS-MISC Exercise
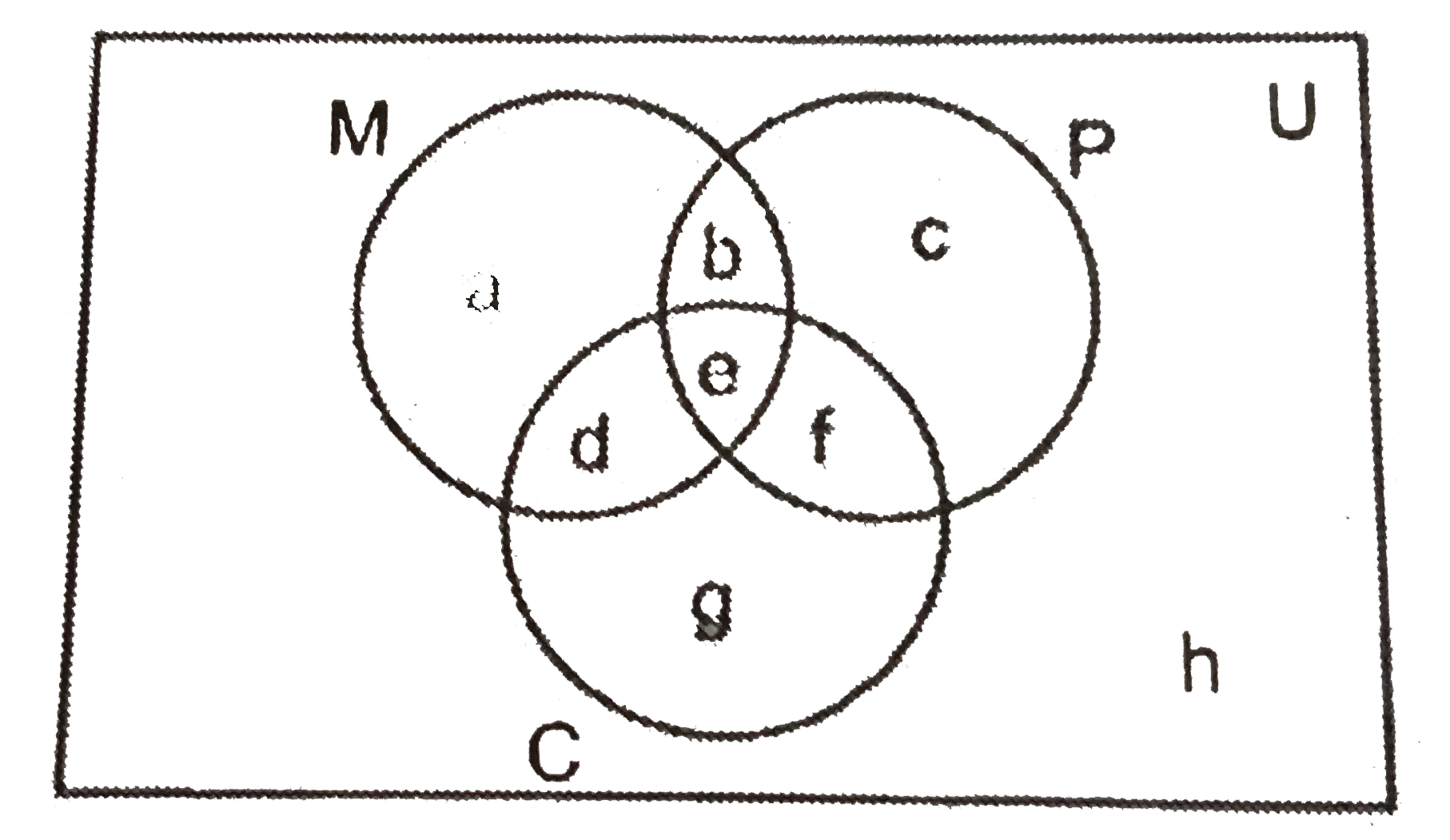
- There are 175 students in a class, out of which 100 students opt Maths...
Text Solution
|
- Decide among the following sets, which are subsets of which: A={x : x ...
Text Solution
|
- In each of the following, determine whether the statement is true or f...
Text Solution
|
- Let A, B and C be the sets such that A uu B=A uu C and A nn B = A nn C...
Text Solution
|
- Show that the following four conditions are equivalent : (i) A sub B...
Text Solution
|
- Show that if A subB , then (C - B)sub(C - A) .
Text Solution
|
- Assume that P (A) = P (B). Show that A = B
Text Solution
|
- Is it true that for any sets A and B, P (A) uuP (B) = P (Auu B)? Just...
Text Solution
|
- Show that for any sets A and B,A = (A nnB) uu(A B )and A uu(B A) = (...
Text Solution
|
- Using properties of sets, show that (i) A uu ( A nn B) = A (ii) A ...
Text Solution
|
- Show that A nn B=A nn C need not imply B=C
Text Solution
|
- Let A and B be sets. If A nnX = B nnX =varphiand A uuX = B uuXfor som...
Text Solution
|
- Find sets A, B and C such that A nnB , B nnC and A nnC are nonempty ...
Text Solution
|
- In a survey of 600 students in a school, 150 students were found to...
Text Solution
|
- In a group of students, 100 students know Hindi, 50 know English an...
Text Solution
|
- In a survey of 60 people, it was found that 25 people read newspaper...
Text Solution
|
- In a survey it was found that 21 people liked product A, 26 liked pr...
Text Solution
|