A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KVPY PREVIOUS YEAR-KVPY-Part 2 Mathematics
- Let g : N ->N with g(n) being the product of the digits of n.(a) Prove...
Text Solution
|
- Let m (respectively, n) be the number of 5-digit integers obtained by ...
Text Solution
|
- The number of solid cones with integer radius and integer height each ...
Text Solution
|
- Let ABCD be a square. An arc of a circle with A as centre and AB as ra...
Text Solution
|
- Suppose ABCD is a trapezium whose sides and height are integers and AB...
Text Solution
|
- Let a, b, c be non-zero real numbers such that a+b+c=0," let "q=a^(2)+...
Text Solution
|
- The value of sum(n=0)^(1947) 1/(2^(n)+sqrt(2^(1947))) is equal to
Text Solution
|
- The number of integers a in the interval [1, 2014] for which the syste...
Text Solution
|
- In a triangle ABC with angleA=90^(@), P is a point on BC such that PA ...
Text Solution
|
- The number of all 3-digit numbers abc (in base 10)for which (axxbxxc...
Text Solution
|
- Let ABCD be a trapezium with parallel sides AB and CD such that the ci...
Text Solution
|
- Let S be the set of all points ((a)/(b),(c)/(d)) on the circle with ra...
Text Solution
|
- Suppose we have two circles of radius 2 each in the plane such that th...
Text Solution
|
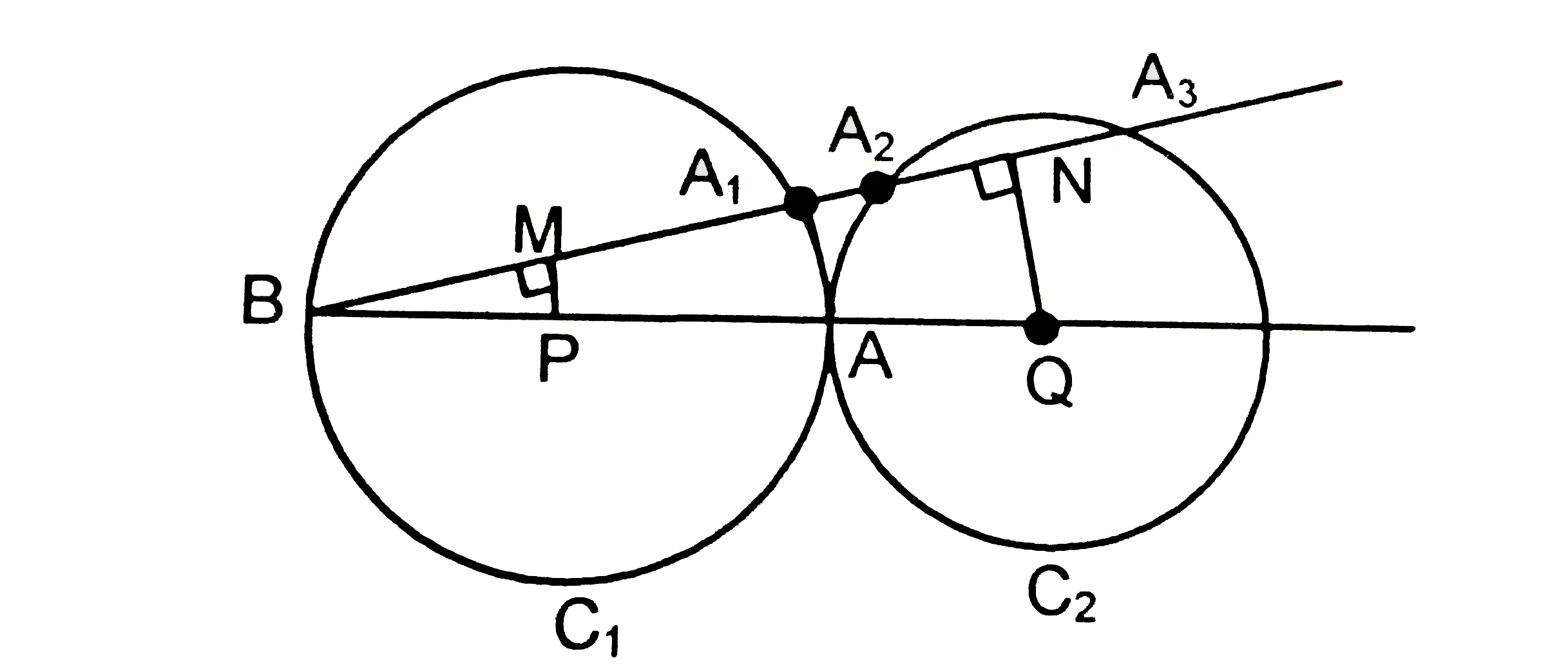
- Let C(1), C(2) be two circles touching each other externally at the p...
Text Solution
|
- Let a, b, c, d be real numbers between - 5 and 5 such that |a|=sqrt(4-...
Text Solution
|