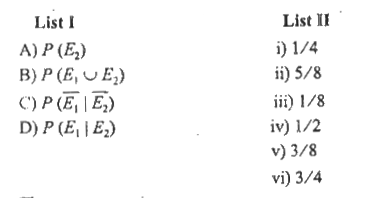Home
Class 12
MATHS
Suppose that E1 and E2 are two events of...

Suppose that `E_1` and `E_2` are two events of a random experiment such that `P(E_(1))=1/4 , P(E_2 |E_2) =1/2 and P(E_1 |E_2)=1/4`. Observe the lists given below :

The correct matching of the list I from the list II is :

A

A-ii, B-iiii, C-vi, D-i

B

A-iv, B-v, C-vi, D-i

C

A-iv, B-ii , C-vi, D-i

D

A-I, B-ii, C-iii, D-iv

Text Solution

Verified by Experts

The correct Answer is:
C
Promotional Banner

Topper's Solved these Questions

  • PROBABILITY

    DIPTI PUBLICATION ( AP EAMET)|Exercise EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-4|5 Videos

  • PROBABILITY

    DIPTI PUBLICATION ( AP EAMET)|Exercise EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-2|8 Videos

  • PERMUTATIONS & COMBINATIONS

    DIPTI PUBLICATION ( AP EAMET)|Exercise EXERCISE 2 ( SPECIAL TYPE QUESTIONS ) SET -4|10 Videos

  • PRODUCTS OF VECTORS

    DIPTI PUBLICATION ( AP EAMET)|Exercise Exercise 2 (Special Type Questions) SET -D|14 Videos

Similar Questions

Explore conceptually related problems

Suppose A and B are events of a random experiment such that P(A) = 1/3 , P (A cap B) = 1/5 and P(A cup B) = 3/5 . Then, match the items of List-I with the items of List-II

E_(1) , E_(2) are events of a sample space such that P(E_(1))=(1)/(4) , P((E_(2))/(E_(1)))=(1)/(2) , P((E_(1))/(E_(2)))=(1)/(4) then P((barE_(1))/(E_(2)))=

The two events E_(1), E_(2) are such that P(E_(1)uuE_(2))=5/8, P (bar(E)_(1))=3/4, P(E_(2))=1/2 , then E_(1) and E_(2) are

If E and F are events such that P(E) = 1/4, P(F) = 1/2 and P(E and F) = 1/8 , find (i) P(E or F), (ii) P(not E and not F).

If E_(1), E_(2) are independent events in a random experiment with P(E_(1) cap E_(2)) =1//8 , P(overlineE_(1) cap overlineE_(2)) = 3//8 , then P(E_(1)), P(E_(2)) =

Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E cup F) = 0.2 , find P(E|F) and P(F|E).

E_(1) , E_(2) are events of a sample space such that P(E_(1))=(1)/(4) , P((E_(2))/(E_(1)))=(1)/(2) , P((E_(1))/(E_(2)))=(1)/(4) then P((E_(1))/(E_(2)))+P((E_(1))/(barE_(2)))=