Home
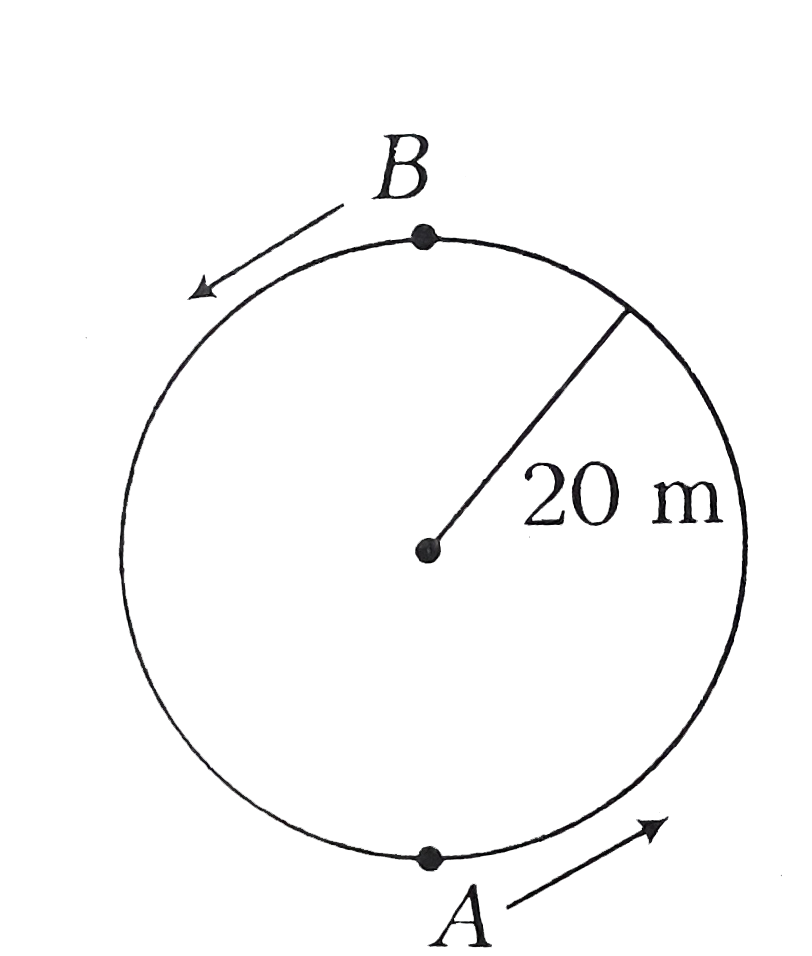
Class 11
PHYSICS
A boy is running over a circular track w...

A boy is running over a circular track with uniform speed of `10 ms^(-1)`. What is the average velocity for movement of boy from A to (in `ms^(-1)`) ?

A

`(10)/(pi)`

B

`(40)/(pi)`

C

10

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
D
`upsilon_(av)=("Displacement")/("Time")=(2R)/((piR//upsilon))=(2upsilon)/(pi)=(20)/(pi)ms^(-1)`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN A PLANE

    DC PANDEY|Exercise Check point 3.3|10 Videos

  • MOTION IN A PLANE

    DC PANDEY|Exercise Check point 3.4|15 Videos

  • MOTION IN A PLANE

    DC PANDEY|Exercise Check point 3.1|10 Videos

  • MOTION

    DC PANDEY|Exercise Medical entrances gallery|19 Videos

  • PROJECTILE MOTION

    DC PANDEY|Exercise Level - 2 Subjective|10 Videos

Similar Questions

Explore conceptually related problems

A train of weight 10^(7)N is running on a travel track with uniform speed of 36 km h^(-1) . The frictional force is 0.5 kg f per quintal. If g = 10 ms^(-2) , power of engine is

A particle is moving on a circular path of radius 10m with uniform speed of 4ms^(-1) .The magnitude of change in velocity of particle when it completes a semi circular path is

A particle is moving on a circular track of radius 30 cm with a constant speed of 6ms^(-1) . Its acceleration is

A particle is moving along a circular along a circular path of radius 5 m with a uniform speed 5ms^(-1) . What will be the average acceleration when the particle completes half revolution?

A man is running away from a plane mirror at the speed of 5 ms^(-1) . With what speed is he receding from his own image ?

When a car runs on a circular track with a uniform speed, its velocity is said to be changing. This is because :

A circular wheel of 0.50 m radius is moving with a speed of 10 ms^(-1) . Find the angular speed.

Three boys are running on a equitriangular track with the same speed 5 ms^(-1) . At start, they were at the three corners with velocity along indicated directions. The velocity of approach of any one of them towards another at t = 10 s equals