A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-LAWS OF MOTION-Check point 5.2
- Four forces act on a point object. The object will be in equilibrium, ...
Text Solution
|
- A block of mass 10 kg is suspended by three strings as shown in figure...
Text Solution
|
- An object is resting at the bottom of two strings which are inclined a...
Text Solution
|
- The pulleys and strings shown in the figure are smooth and of negligib...
Text Solution
|
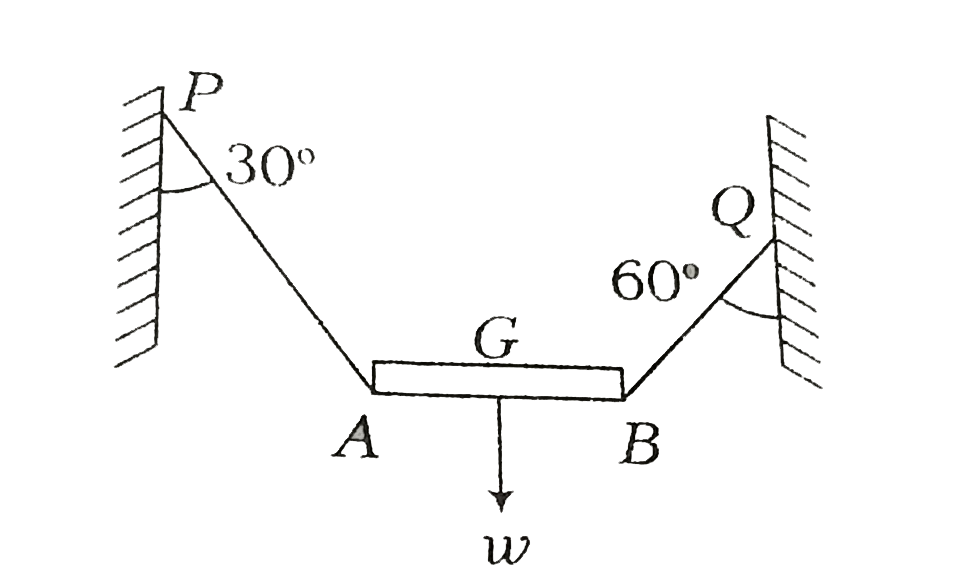
- A non-uniform rod AB of weight w is supported horizontally in a vertic...
Text Solution
|
- A weight w is suspended from the midpoint of a rope, whose ends are at...
Text Solution
|
- The adjacent figure is the part of a horizontally stretched net. secti...
Text Solution
|
- Two particles of equal mass are connected to a rope AB of negligible m...
Text Solution
|
- When a force F acs on a body of mass m the acceleration product in the...
Text Solution
|
- Three forces acting on a body are shown in figure. To have the resulta...
Text Solution
|
- Two equal forces are acting at a point with an angle 60^(@) between th...
Text Solution
|
- A body of mass 60 kg suspended by means of three strings, P, Q and R a...
Text Solution
|
- A body is under the action of two mutually perpendicular forces of 3 N...
Text Solution
|
- A ball of mass 1kg hangs in equilibrium from two strings as shown in I...
Text Solution
|
- A mam of mass 50 g stands on a frame of mass 30 g. He pulls on a light...
Text Solution
|