Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
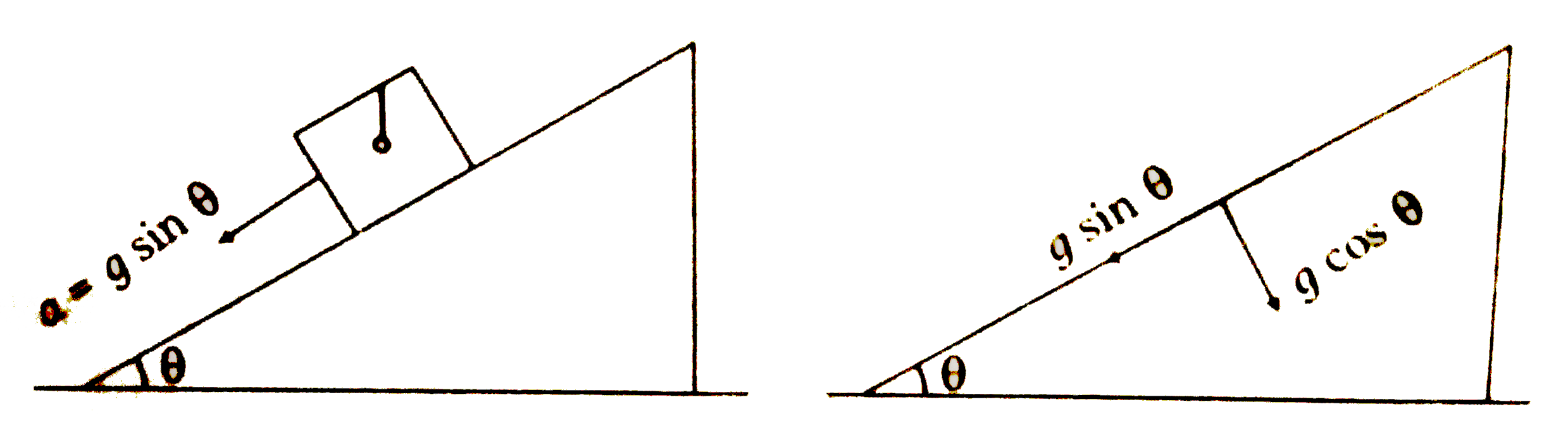
- A simple pendulum of length l is suspended from the celing of a cart ...
Text Solution
|
- The period of oscillation of a simple pendulum of length (L) suspended...
Text Solution
|
- A simple pendulum of length l is suspended from the celing of a cart w...
Text Solution
|
- Find the period of oscillation of a simple pendulum of length L suspen...
Text Solution
|
- The period of oscillation of a simple pendulum of length l suspended f...
Text Solution
|
- A simple pendulum is suspended from the roof of a vehicle which on an ...
Text Solution
|
- Find the period of oscillation of a simple pendulum of length L suspen...
Text Solution
|
- The period of oscillation of a simple pendulum of length L suspended f...
Text Solution
|
- The period of oscillation of a simple pendulum of length 'L' suspended...
Text Solution
|