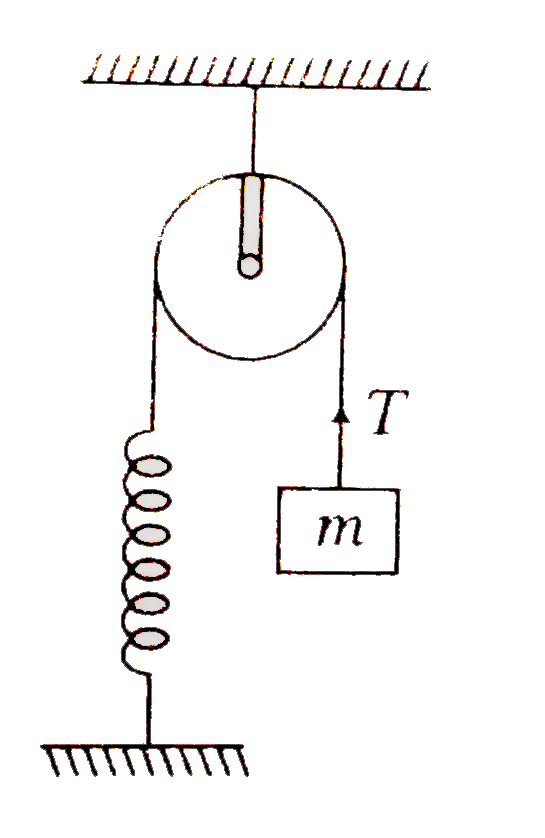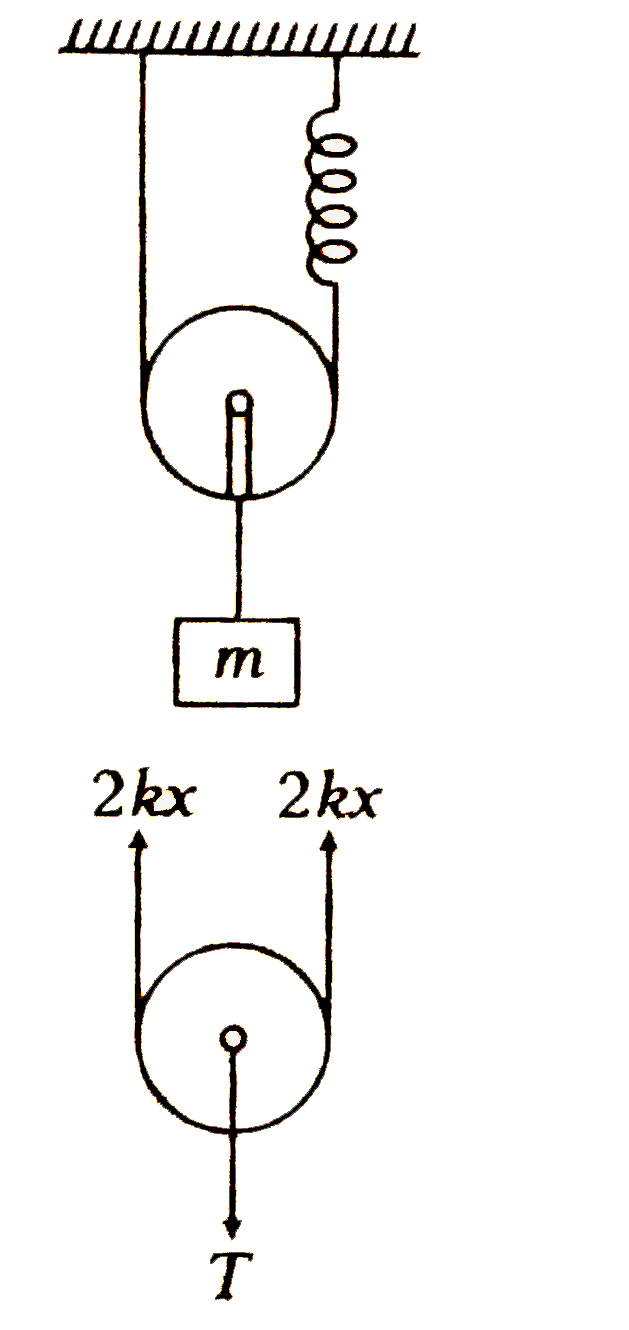Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the following arrangements, bock is slightly displaced vertically d...
Text Solution
|
- A block of mass m hangs from a vertical spring of spring constant k. I...
Text Solution
|
- Figure shows a system consisting of a massles pulley, a spring of forc...
Text Solution
|
- In the following arrangements, bock is slightly displaced vertically d...
Text Solution
|
- In the device shown in Fig, the block m is displaced down slightly and...
Text Solution
|
- Figure shows a system consisting of a massless pulley, a spring of for...
Text Solution
|
- Find the time period of mass M when displaced from its equilibrium pos...
Text Solution
|
- Figure shows a system consisting of a massless pulley, a spring of for...
Text Solution
|
- A system shown in the figure consists of a massless pulley, a spring o...
Text Solution
|