Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
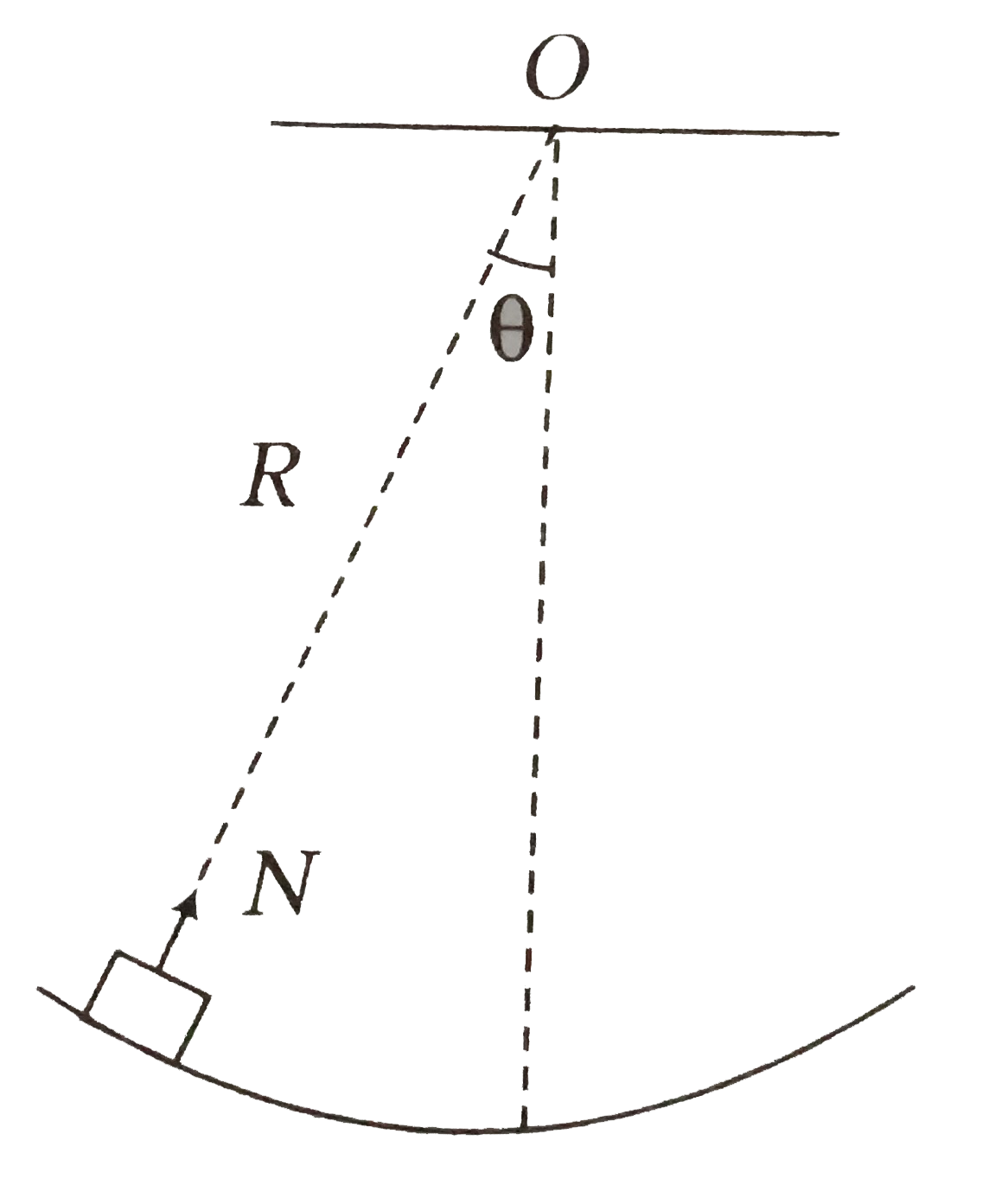
- A small block oscillates back and forth on a smooth concave surface of...
Text Solution
|
- A small block oscillates back and forth on as smooth concave surface o...
Text Solution
|
- A spherical ball of mass m and radius r rolls without slipping on a ro...
Text Solution
|
- A system is shown in the figure. The force The time period for small ...
Text Solution
|
- A small block oscillates back and forth on a smooth concave surface of...
Text Solution
|
- A uniform ring of radius 'R' is suspended from a horizontal nail 'A' a...
Text Solution
|
- If in the above problem the block is replaced by a small spherical bal...
Text Solution
|
- एक छोटा ब्लॉक एक चिकनी अवतल सतह पर फिसलता हुआ छोटे आयाम के साथ दोलन कर...
Text Solution
|
- एक गोलाकार बॉल का द्रव्यमान m तथा त्रिज्या r है। यह एक घर्षणयुक्त अवतल...
Text Solution
|