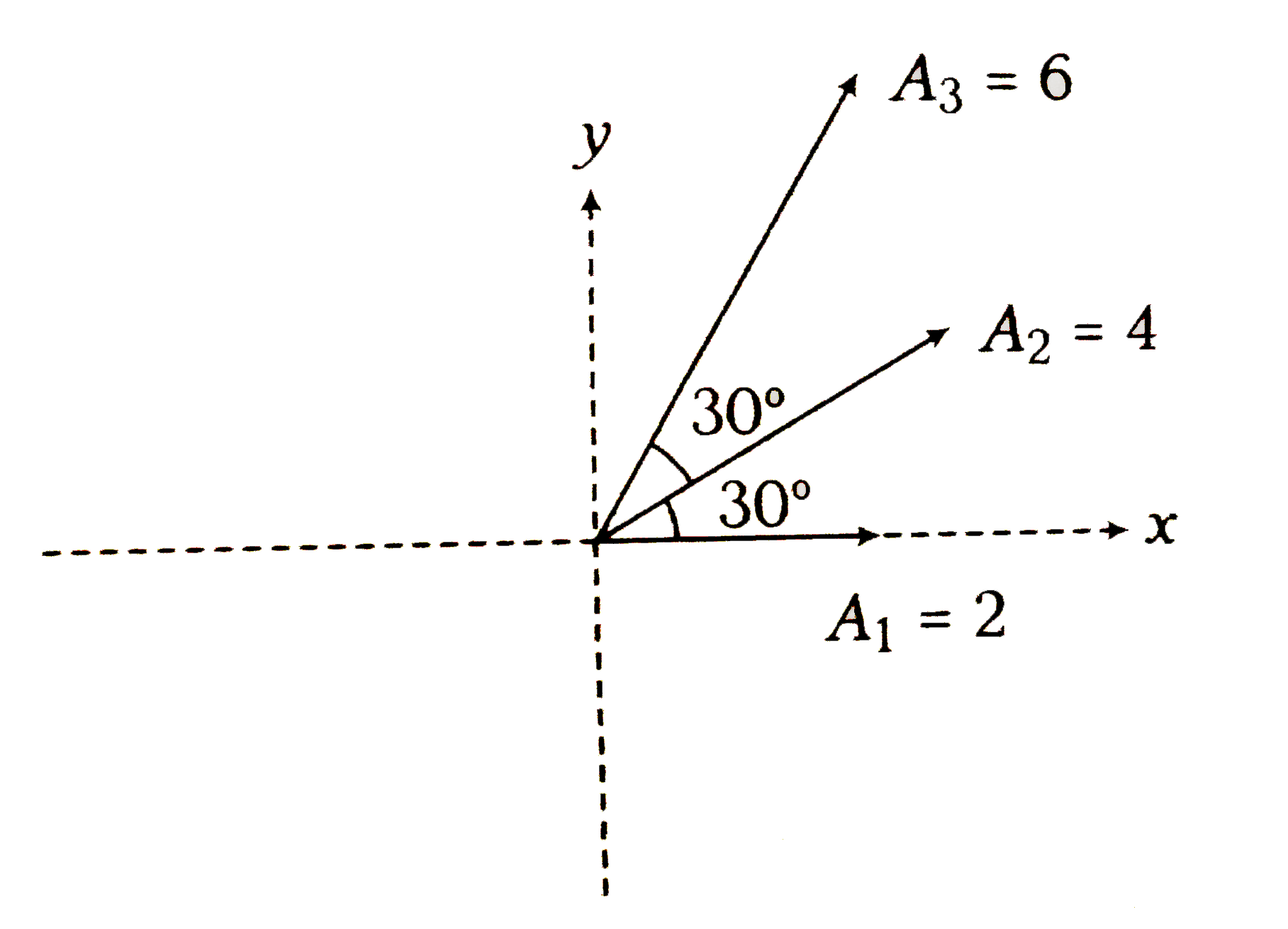
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the displacement equation of the simple harmonic motion obtained ...
Text Solution
|
- Find the displacement equation of the simple harmonic motion obtained ...
Text Solution
|
- Four simple harmonic motions , c(1)=8sinomegat,x(2)=6sin(omegat=pi//2)...
Text Solution
|
- Using graphical means find an amplitude a of oscillations resulting fr...
Text Solution
|
- Four simple harmonic vibrations x(1) = 8s "in" (omegat), x(2) = 6 si...
Text Solution
|
- x(1)=A sin (omegat-0.1x) and x(2)=A sin (omegat-0.1 x-(phi)/2) Resulta...
Text Solution
|
- Find the displacement equation of the simple harmonic motion obtained ...
Text Solution
|
- What is the phase difference between two simple harmonic motions repre...
Text Solution
|
- x(1) = 5 sin (omegat + 30^(@)) x(2) = 10 cos (omegat) Find amplitu...
Text Solution
|