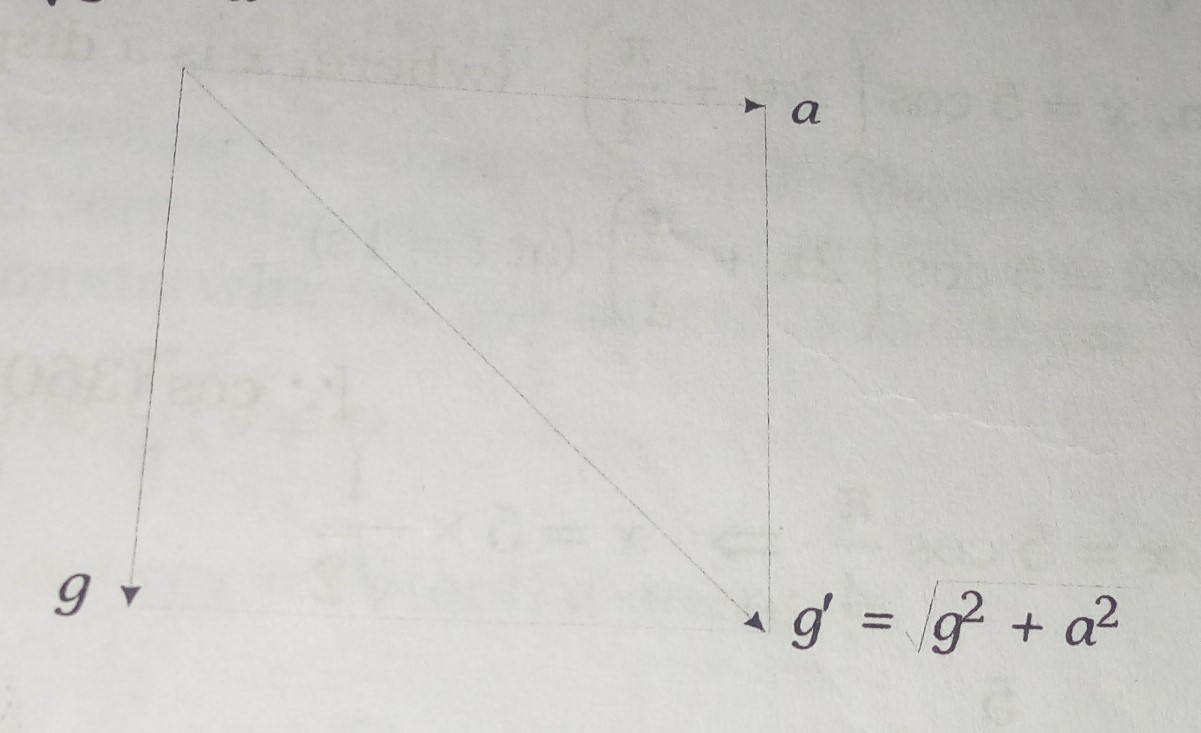A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A simple pendulum is suspended from the roof of a trolley which moves ...
Text Solution
|
- A simple pendulum is suspended from the roof of a trolley which moves ...
Text Solution
|
- A simple pendulum of length L is suspended from the roof of a train. I...
Text Solution
|
- A simple pendulum is suspended from the roof of a school bus which mov...
Text Solution
|
- A simple pendulum is suspended from the roof of a school bus which mov...
Text Solution
|
- A simple pendulum is suspended from the roof of a school bus which mov...
Text Solution
|
- A simple pendulum is suspended from the roof of a school bus which mov...
Text Solution
|
- A simple penduulum of length l is suspended from the roof of a train w...
Text Solution
|
- एक सरल लोलक ट्रॉली की छत से लटका हुआ है। ट्रॉली क्षैतिज सीधा म...
Text Solution
|