Home
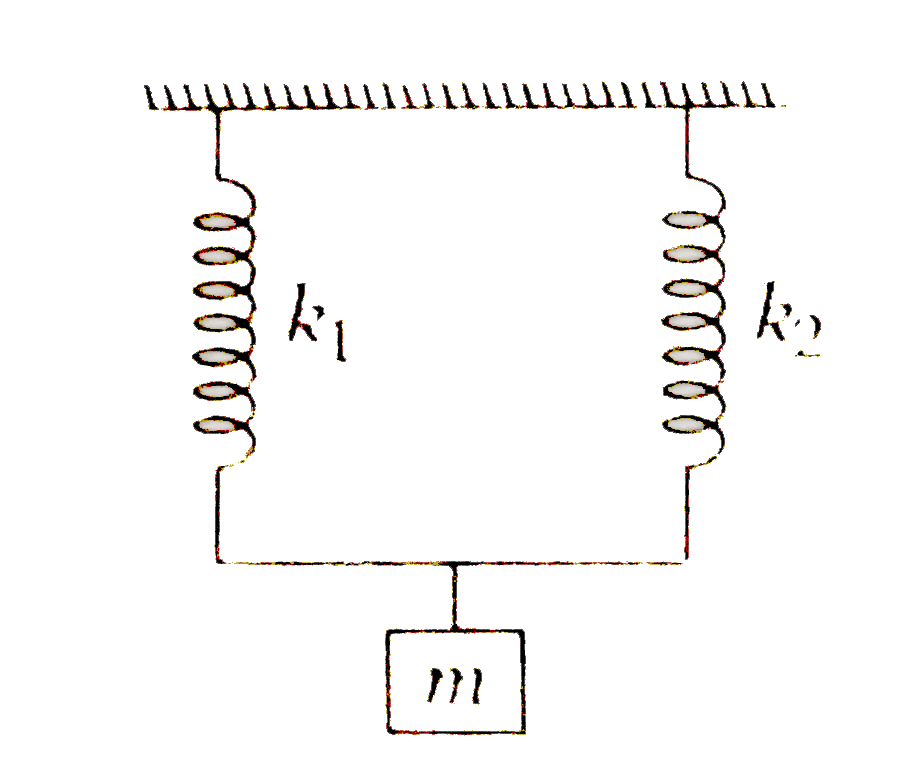
Class 11
PHYSICS
The spring constants of two springs of s...

The spring constants of two springs of same length are `k_(1)` and `k_(2)` as shown in figure. If an object of mass m is suspended and set in vibration , the period will be

A

`2pisqrt((mk_(1))/(k_(2)))`

B

`2pisqrt((m)/(k_(1)k_(2)))`

C

`2pisqrt((m)/(k_(1)-k_(2)))`

D

`2pisqrt(m//(k_(1)+k_(2)))`

Text Solution

Verified by Experts

The correct Answer is:
D
(d) The springs are corrected in parallel. So, the efffective force constant will be `k_(e)=k_(1)+k_(2)`
`therefore T=2pisqrt((m)/(k_(e)))=2pisqrt((m)/(k_(1)+k_(2))`
Promotional Banner

Similar Questions

Explore conceptually related problems

Two identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be

Two identical spring of constant K are connected in series and parallel as shown in figure. A mass mis suspended from them. The ratio of their frequencies of vertical oscillations will be

Two spring of spring constants k_(1) and k_(2) ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

A spring of force constant k is cut into two parts whose lengths are in the ratio 1:2 . The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is

A block of mass m is connected between two springs (constants K_(1) and K_(2) ) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

A system consists of two spring and a mass m = 1 kg as shown in figure . If mass m is dispalced slightly along vertical and vertical and released. The system oscillates with a period of 2 s .Then , the spring canstant K is

A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k_(1) and k_(2) respectively. When set into vertical vibrations, the period will be

A mass m is suspended by means of two coiled spring which have the same length in unstretched condition as in figure. Their force constant are k 1 and k 2 respectively. When set into vertical vibrations, the period will be