Home
Class 11
PHYSICS
A particle of mass m oscillates with sim...

A particle of mass m oscillates with simple harmonic motion between points `x_(1)` and `x_(2)`, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph

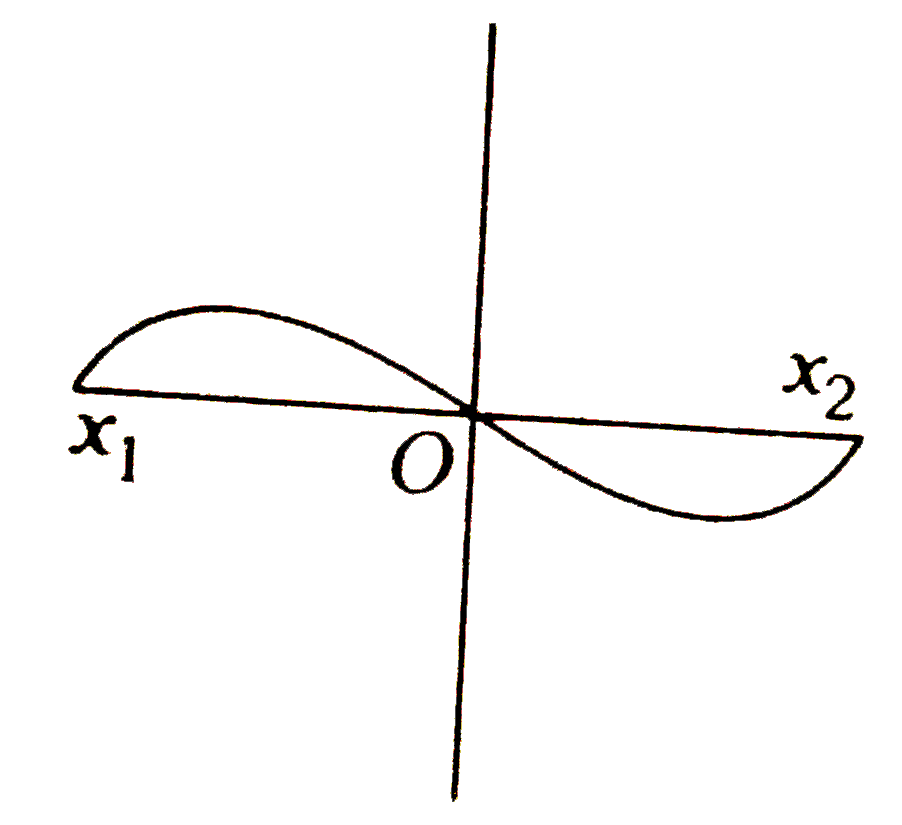
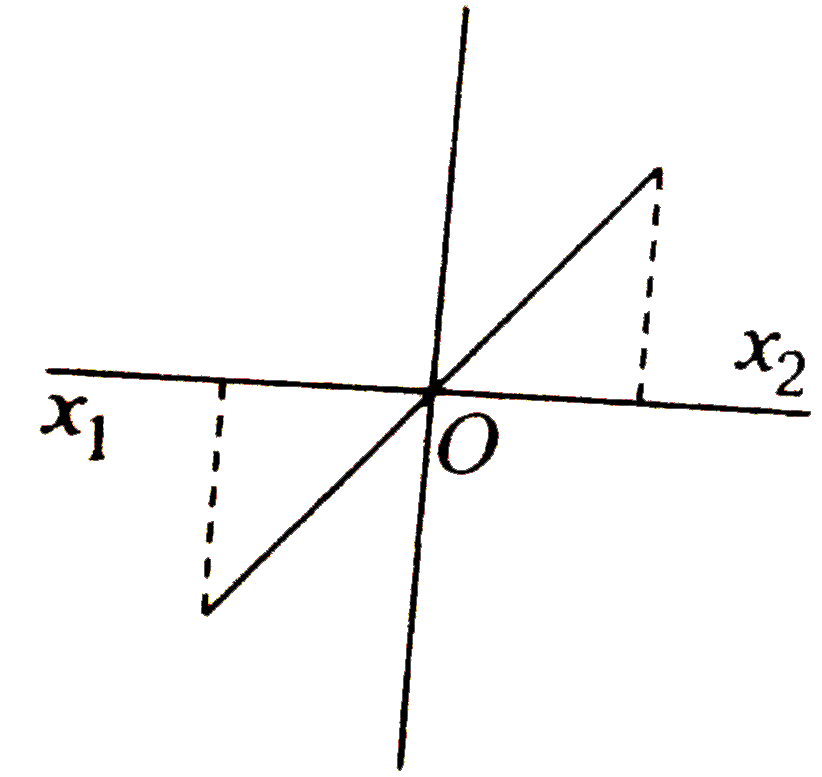
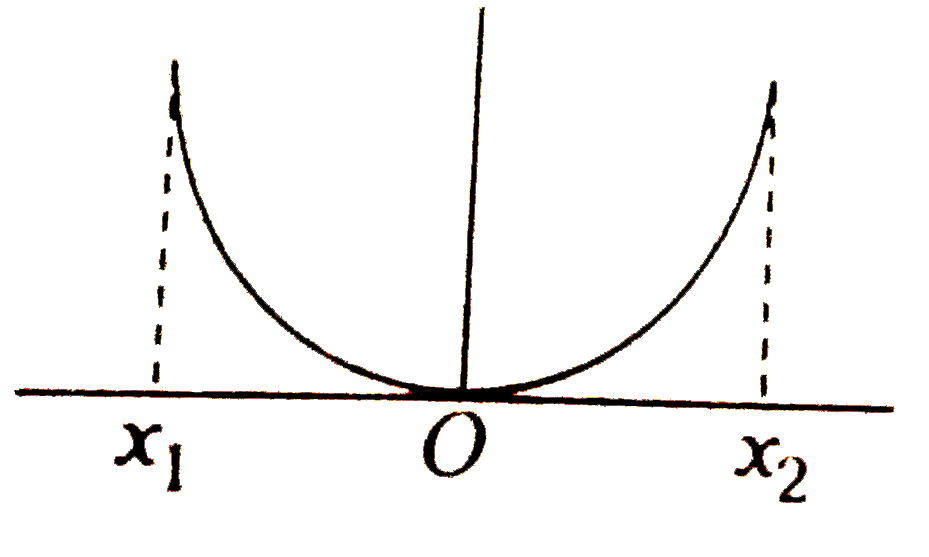
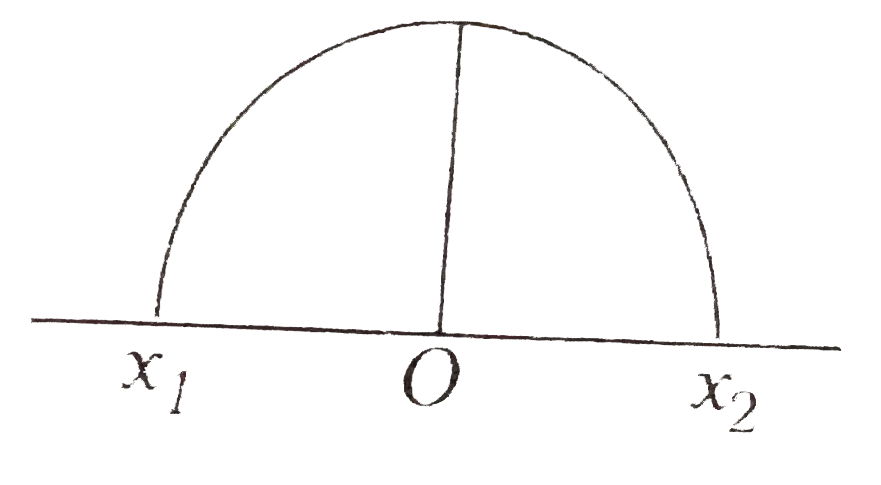
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
(c) Potential energy graph is parabolic with its minimum value at mean position.
Promotional Banner

Similar Questions

Explore conceptually related problems

A particle of mass m oscillates with simple harmonic motion between points x_(1) and x_(2) the equilibrium position being O its potential energy in plotted it will be as given bellow in the graph

The potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to

A particle executes simple harmonic motion of ampliltude A. At what distance from the mean position is its kinetic energy equal to its potential energy?

A particle oscillates simple harmonic motion with a period of 16 s . Two second after crossing the equilibrium position its velocity becomes 1 m//s . The amplitude is

A particle is executing simple harmonic motion between exterme positions given by (-1,-2,-3)cm and (1,2,1)cm . Its amplitude of oscillation is

A particle is vibrating in a simple harmonic motion with an amplitude of 4 cm . At what displacement from the equilibrium position, is its energy half potential and half kinetic

A particle starts oscillating simple harmonically from its equilibrium position then, the ration of kinetic energy and potential energy of the particle at the time T//12 is: (T="time period")

When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is