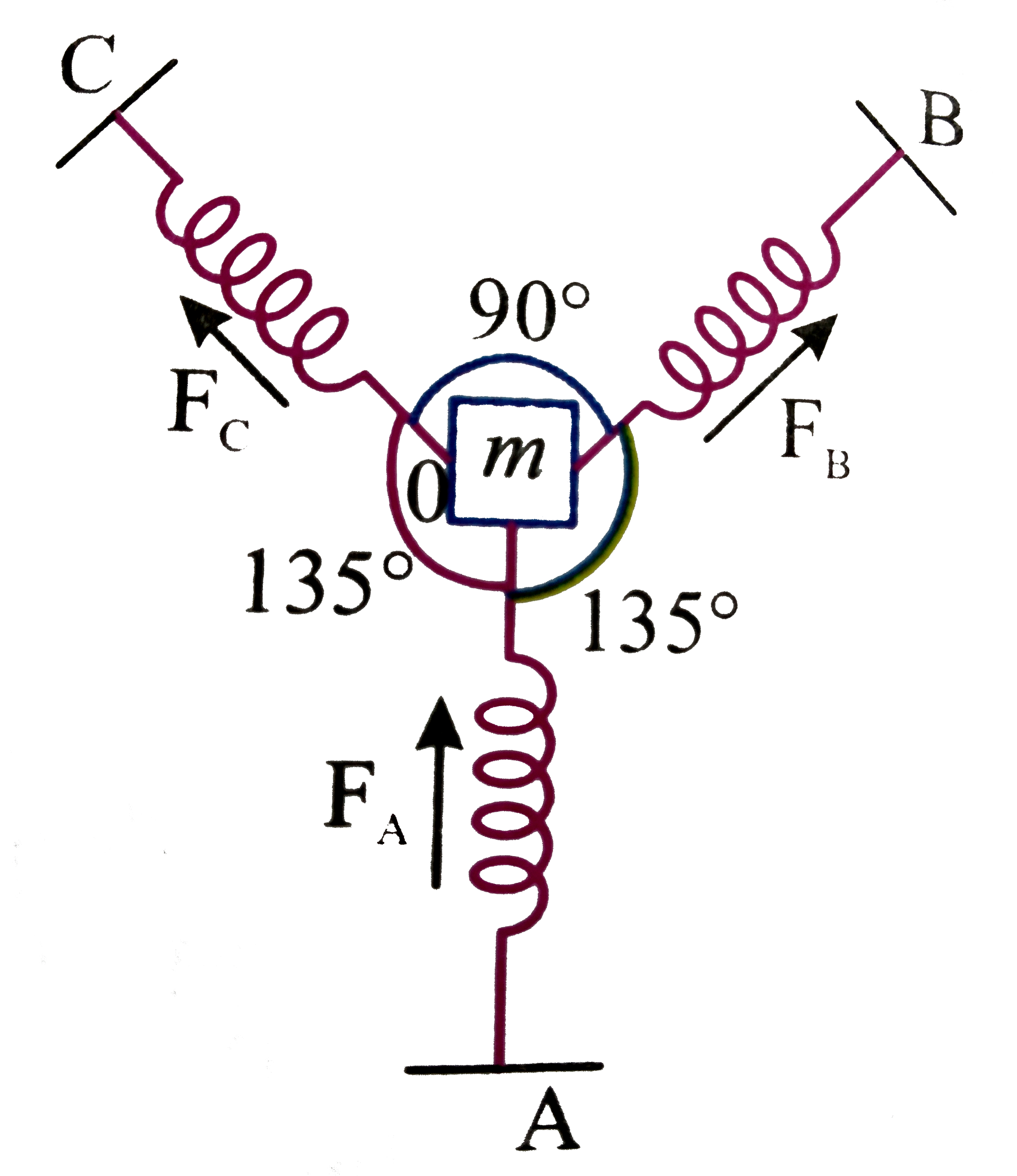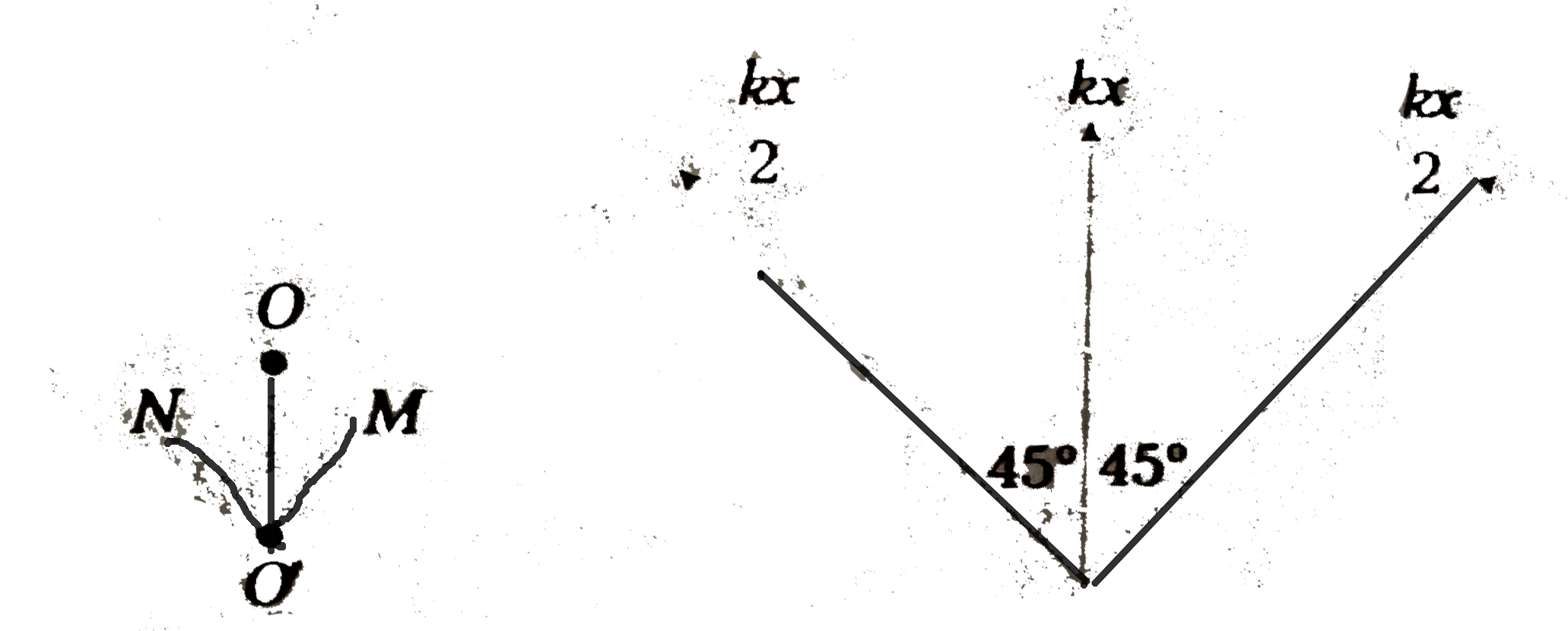A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass 'm' is attached to three identical springs A,B and ...
Text Solution
|
- A particle of mass m is asttached to three springs A,B and C of equla ...
Text Solution
|
- A particle of mass m is attached with three springs A,B and C of equal...
Text Solution
|
- A particle of mass m is attached to three identical springs of spring...
Text Solution
|
- A particle of mass 'm' is attached to three identical springs A,B and ...
Text Solution
|
- A body of mass m is suspended from three springs as shown in figure. I...
Text Solution
|
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- A particle of mass m is attached to four springs with spring constant ...
Text Solution
|
- Three springs of each force constant k are connected as shown figure. ...
Text Solution
|