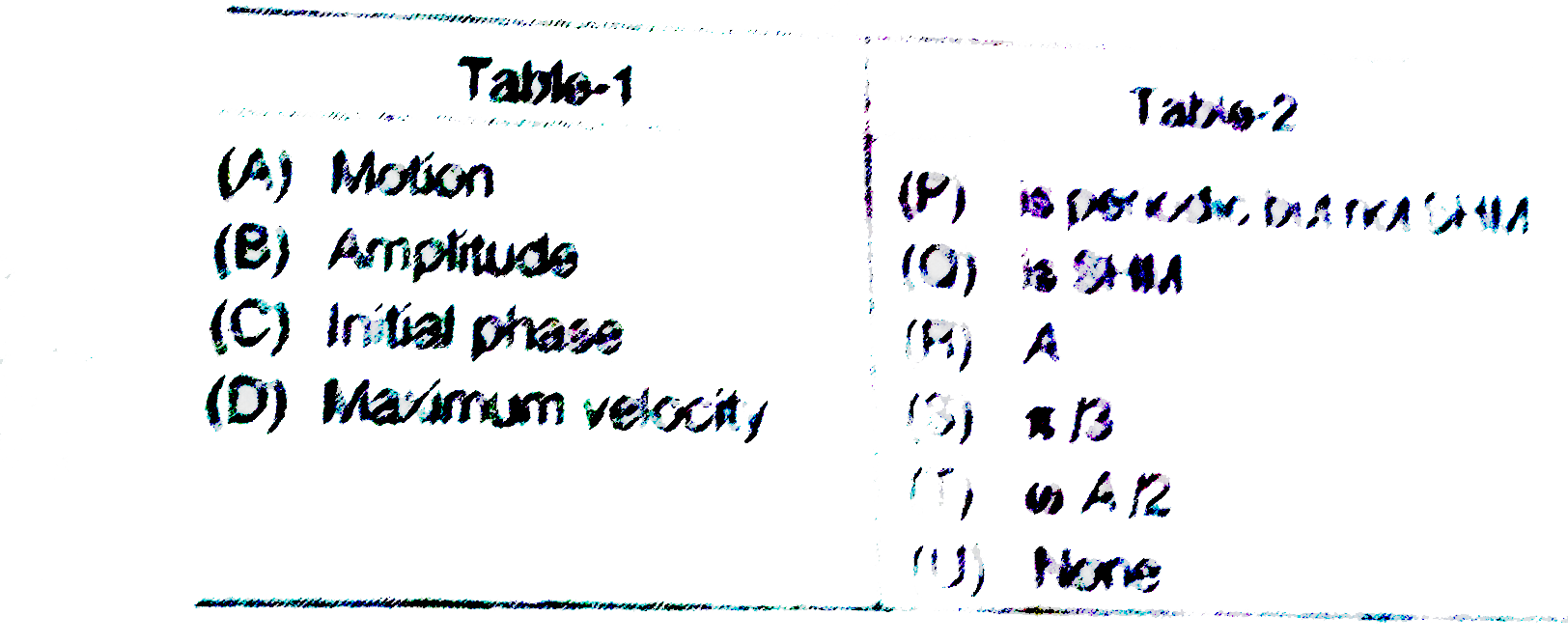Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In y= A sin omegat + A sin (omegat+(2pi)/3) match the following table.
Text Solution
|
- Find the resultant amplitude and the phase difference between the resu...
Text Solution
|
- The amplitude of the vibrating particle due to superposition of two SH...
Text Solution
|
- Find the trajectory equation y(x) of a point if it moves according to ...
Text Solution
|
- Two simple harmonic motions given by, x = a sin (omega t+delta) and y ...
Text Solution
|
- In y= A sin omega t + A sin ( omega t+(2 pi )/3) match the following t...
Text Solution
|
- The equations of two SH M's are X(1) = 4 sin (omega t + pi//2) . X...
Text Solution
|
- The resultant ampiltude of a vibrating particle by the superposition o...
Text Solution
|
- Which two of the following waves are in the same phase? y= A sin (kx...
Text Solution
|