Home
Class 12
PHYSICS
A magnetic needle suspended in a vertica...

A magnetic needle suspended in a vertical plane at `30^@` from the magnetic meridian makes an angle of `45^@` with the horizontal. Find the true angle of dip.

A

approx45^(@) `

B

`30^(@) `

C

`approx41^(@) `

D

approx51^(@) `

Text Solution

Verified by Experts

The correct Answer is:
C
In a vertical plane at `30^(@)` from the magnetic meridian, the horizontal component is,

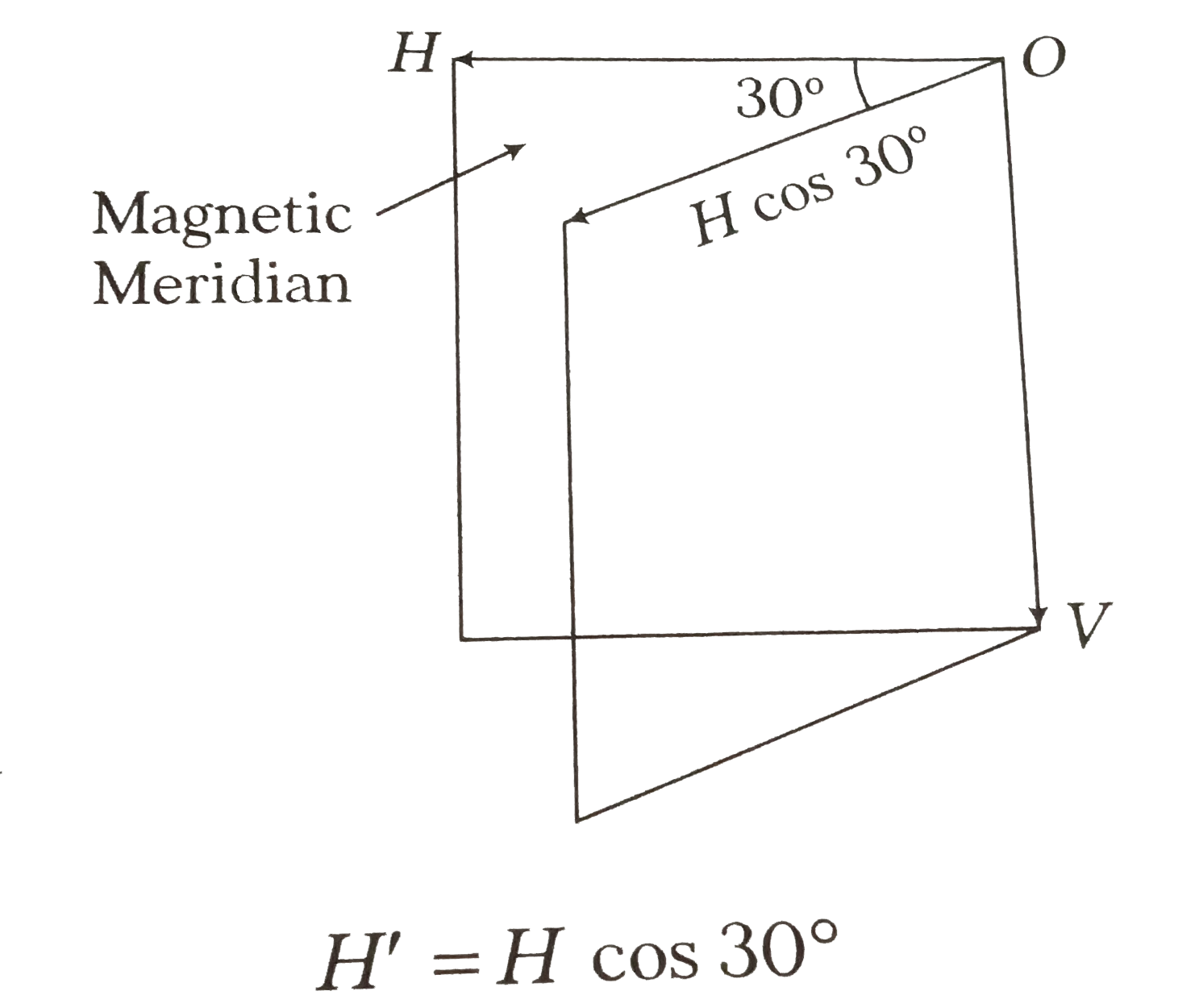
While vertical component is still. Thereofre, apparent dip will be given by `tan theta'=(V)/(H)=(V)/(H cos30^(@))`
`but " " (V)/(H)=tan theta' " " (where theta= "true angle of dip")`
`therefore " " tan theta'=(tan theta)/(cos 30^(@))`
`therefore " " theta=tan^(-1)[tan theta'cos30^(@)] `
`therefore " " a=tan^(-1)[(tan45^(@))(cos30^(@))]approx41^(@) `
Promotional Banner

Topper's Solved these Questions

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise 5.1|14 Videos

  • MAGNETISM AND MATTER

    DC PANDEY|Exercise 5.2|14 Videos

  • MAGNETICS

    DC PANDEY|Exercise MCQ_TYPE|1 Videos

  • MODERN PHYSICS

    DC PANDEY|Exercise Integer Type Questions|17 Videos

Similar Questions

Explore conceptually related problems

If a dip needle is suspended at an angle 30° to the magnetic meridian, it makes an angle of 45^@ with the horizontal. The real dip is

A magnet suspended at 30^@ with magnetic meridian makes an angle of 45^@ with the horizontal. What shall be the actual value of the angle of dip?

If a magnet is suspended at an angle 30∘ to the magnetic meridian and in thisplane the dip needle makes an angle of 60∘ with the horizontal. The true value of dip is

If a magnet is suspended at an angle 30^(@) to the magnetic meridian and in this plane the dip needle makes an angle of 60^(@) with the horizontal. The true value of dip is:

The real angle of dip, if a magnet is suspended at an angle of 30^(@) to the magnetic meridian and the dip needle makes an angle of 45^(@) with horizontal, is:

A magnetic needle free to rotate in a fixed vertical plane stays in a direction making an angle of 60^@ with the horizontal. If the dip at that plane is 37^@ , find the angle of the fixed vertical plane with the meridian.