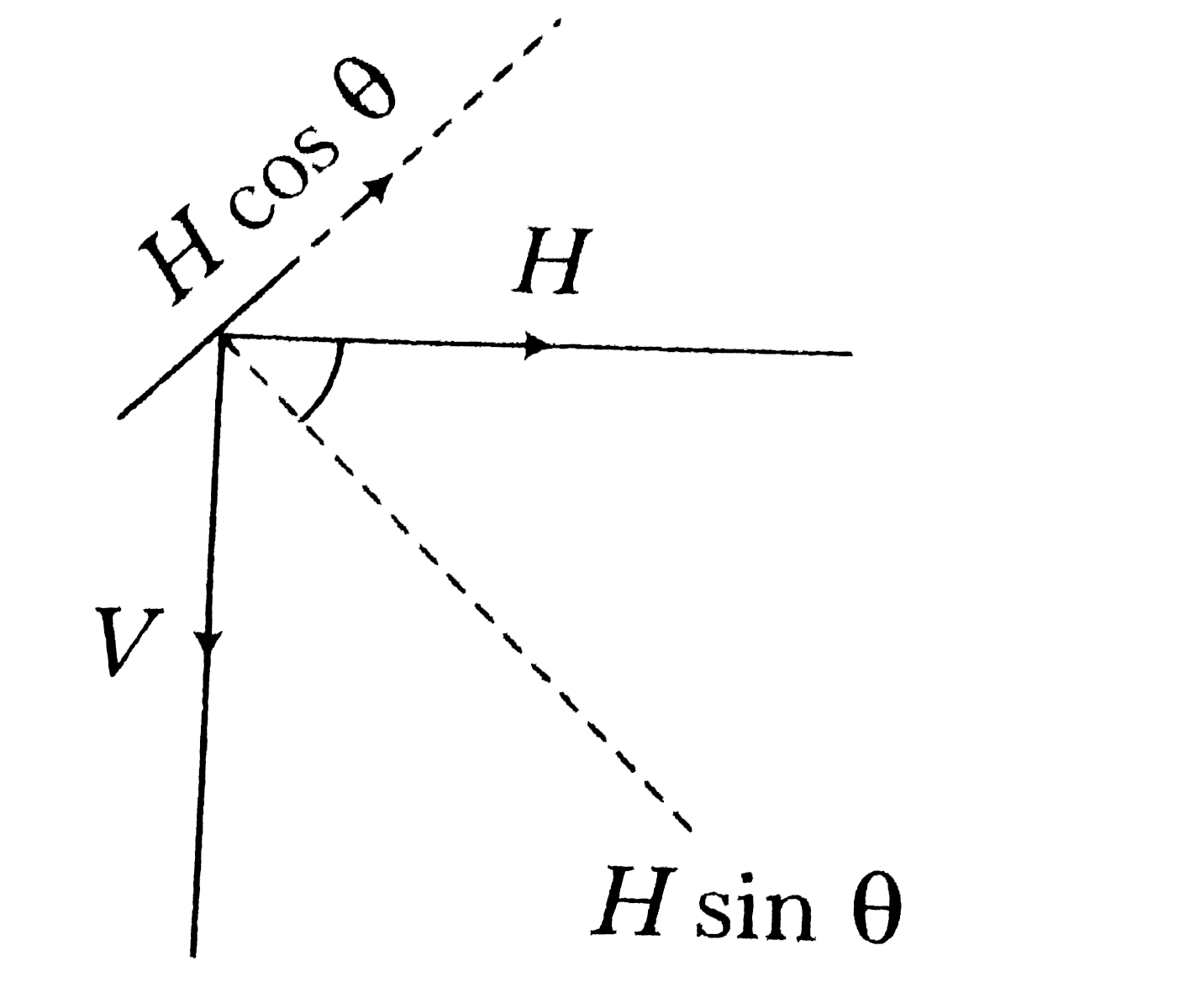
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The plane of dip circle is set in the geographic meridian and the appa...
Text Solution
|
- The plane of dip circle is set in the geographic meridian and the appa...
Text Solution
|
- In a vertical plane p(1) making angle 30^(@) with magnetic meridian , ...
Text Solution
|
- A dip circle is at right angles to the magnetic meridian. What will be...
Text Solution
|
- The original value of the angle of dip at a place is 45^(@) what will...
Text Solution
|
- The original value of the angle of dip at a place is 45^(@) what will...
Text Solution
|
- A dip circle is placed in geographic meridian at a place where dip and...
Text Solution
|
- The vertical plane dip circle is perpendicular to the magnetic meridia...
Text Solution
|
- For a place, the true value of angle of dip is 30^@ . Find the appare...
Text Solution
|