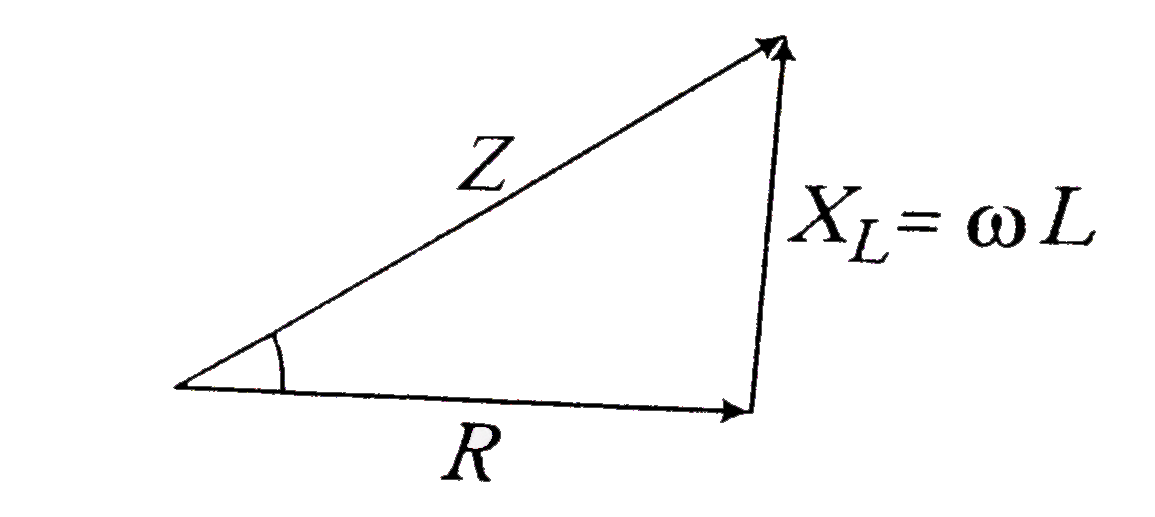
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A 60 cycle AC, circuit has a resistance of 200 Omega and inductor of ...
Text Solution
|
- A series circuit has an impedance of 60.0 Omega and a power factor of ...
Text Solution
|
- A 60 cycle AC circuit has a resistance of 200 Omega and inductance of ...
Text Solution
|
- An inductor 200 mH, capacitor 500mu F and resistor 10 Omega are connec...
Text Solution
|
- An a.c. source is connected across an LCR series circuit with L = 100 ...
Text Solution
|
- A 60 cycle AC, circuit has a resistance of 200 Omega and inductor of 1...
Text Solution
|
- A circuit draws 330 W from a 110 V , 60 Hz AC line. The power factor i...
Text Solution
|
- A circuit draws 280 W from a 110V, 60Hz ac line. The current lags the ...
Text Solution
|
- A circuit draws a power of 600 W from an AC source of 200 V 50 Hz . Th...
Text Solution
|