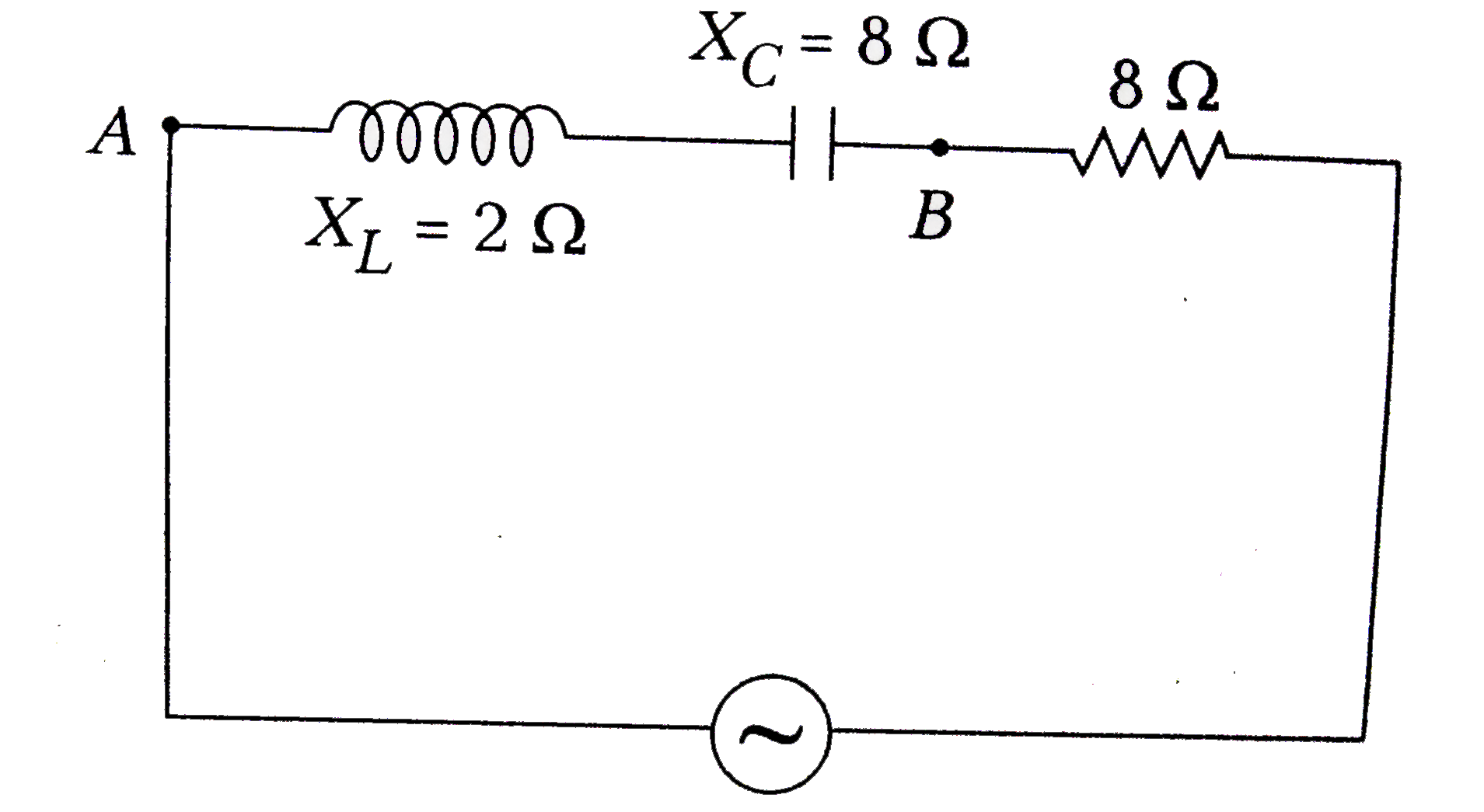A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An inductor X(L) = 2Omega ) , a capacitor (X(C) = 8Omega) and a resist...
Text Solution
|
- A 0.21 H inductor and a 12 Omega resistance are connected in series t...
Text Solution
|
- An alternating voltage V = 100 sin omega t is applied across an LCR ci...
Text Solution
|
- An inductor (X(L) = 2 Omega) a capacitor (X(C ) = 8 Omega) and a resis...
Text Solution
|
- An inductor (L = (1)/(100 pi) H), a capacitor (C = (1)/(500 pi) F) and...
Text Solution
|
- An inductor X(L) = 2Omega ) , a capacitor (X(C) = 8Omega) and a resist...
Text Solution
|
- एक ac वोल्टता को श्रेणीक्रम में जुड़े एक प्रतिरोधक R और एक प्रेरक L पर ...
Text Solution
|
- In an L-R circuit, an inductance of 0.1 H and a resistance of 1 Omega ...
Text Solution
|
- An LCR series circuit having 220 V ac source, inductance L = 25 mH and...
Text Solution
|