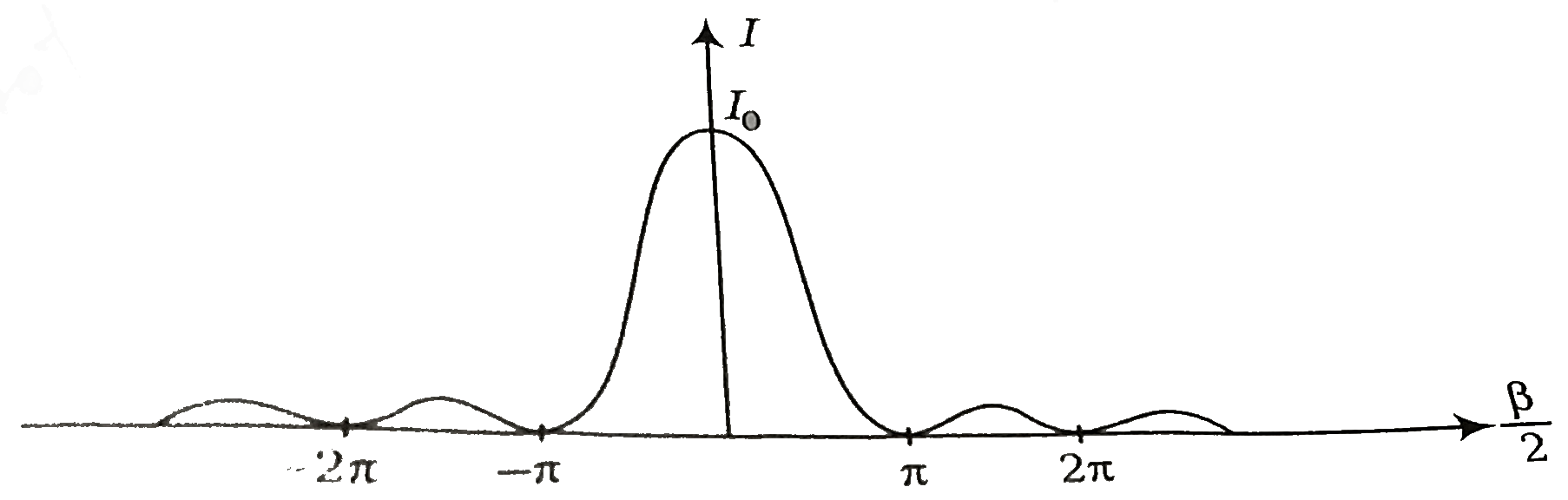
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-WAVE OPTICS-For JEE Advanced E. Integer Type Questions
- Find the ratio of the intensities of the secondary maxima to the inten...
Text Solution
|
- In the Young's double slit experiment, the intensities at two points P...
Text Solution
|
- In Young's double slit experiment, the two slits acts as coherent sour...
Text Solution
|
- Two waves of same frequency and same amplitude from two monochromatic ...
Text Solution
|
- An interference is observed due to two coherent sources separated by a...
Text Solution
|
- Two beam of light having intensities I and 4I interfere to produce a f...
Text Solution
|
- In a Young's experiment, one of the slits is covered with a transparen...
Text Solution
|
- One slit of a double slits experiment is covered by a thin glass plate...
Text Solution
|
- Phase difference at the central point changes by pi//3 when as thick f...
Text Solution
|
- A monchromatic beam of electrons accelerated by a potential difference...
Text Solution
|
- The outer surface of a transparent glass slab of refractive index mu(S...
Text Solution
|
- In a Young's double slit experiment, slits are seperated by a distance...
Text Solution
|
- A parrallel beam of light (lambda=5000Å) is incident at an angle alpha...
Text Solution
|
- In a Young's double slit experiment, one of the slits is covered by a ...
Text Solution
|