Similar Questions
Explore conceptually related problems
Recommended Questions
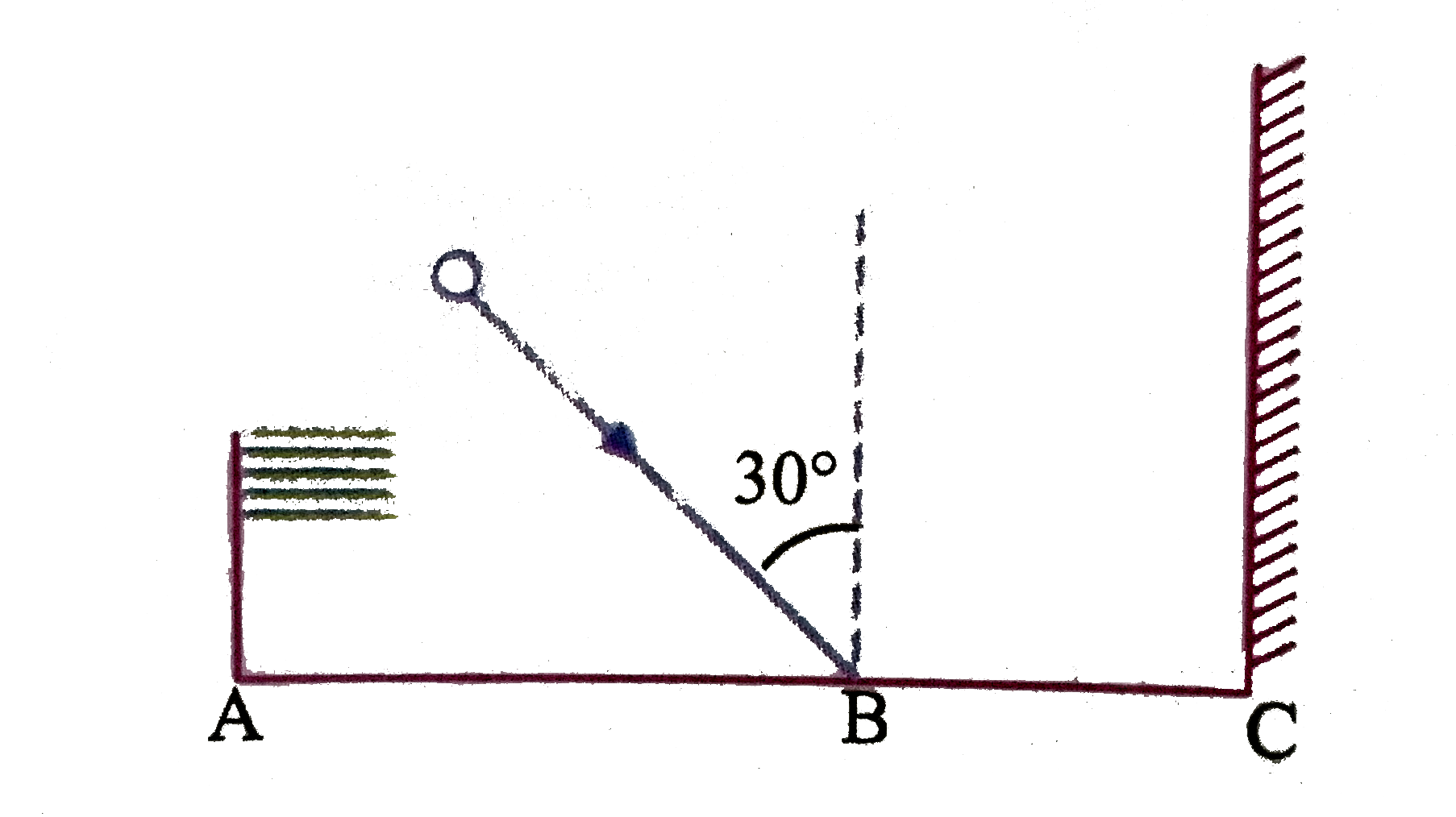
- A ball collides at B with velocity 10m//s at 30^(@) with vertical. The...
Text Solution
|
- A ball collides at B with velocity 10m//s at 30^(@) with vertical. The...
Text Solution
|
- A ping-pong ball strikes a wall with a velocity of 10 ms^(-1). If the ...
Text Solution
|
- A ball of mass M moving with a velocity v collides perfectly inelastic...
Text Solution
|
- A ball collides with a frictionless wall with velocity u as shown in t...
Text Solution
|
- A ball moving vertically downward with a speed of 10 m//s collides wit...
Text Solution
|
- A ball of mass m moving with a speed u(1) collides elasticity with ano...
Text Solution
|
- A ball A of mass M collides elastically with a similar ball B at rest ...
Text Solution
|
- A ball moving with speed u collides with an identical ball at rest. Th...
Text Solution
|