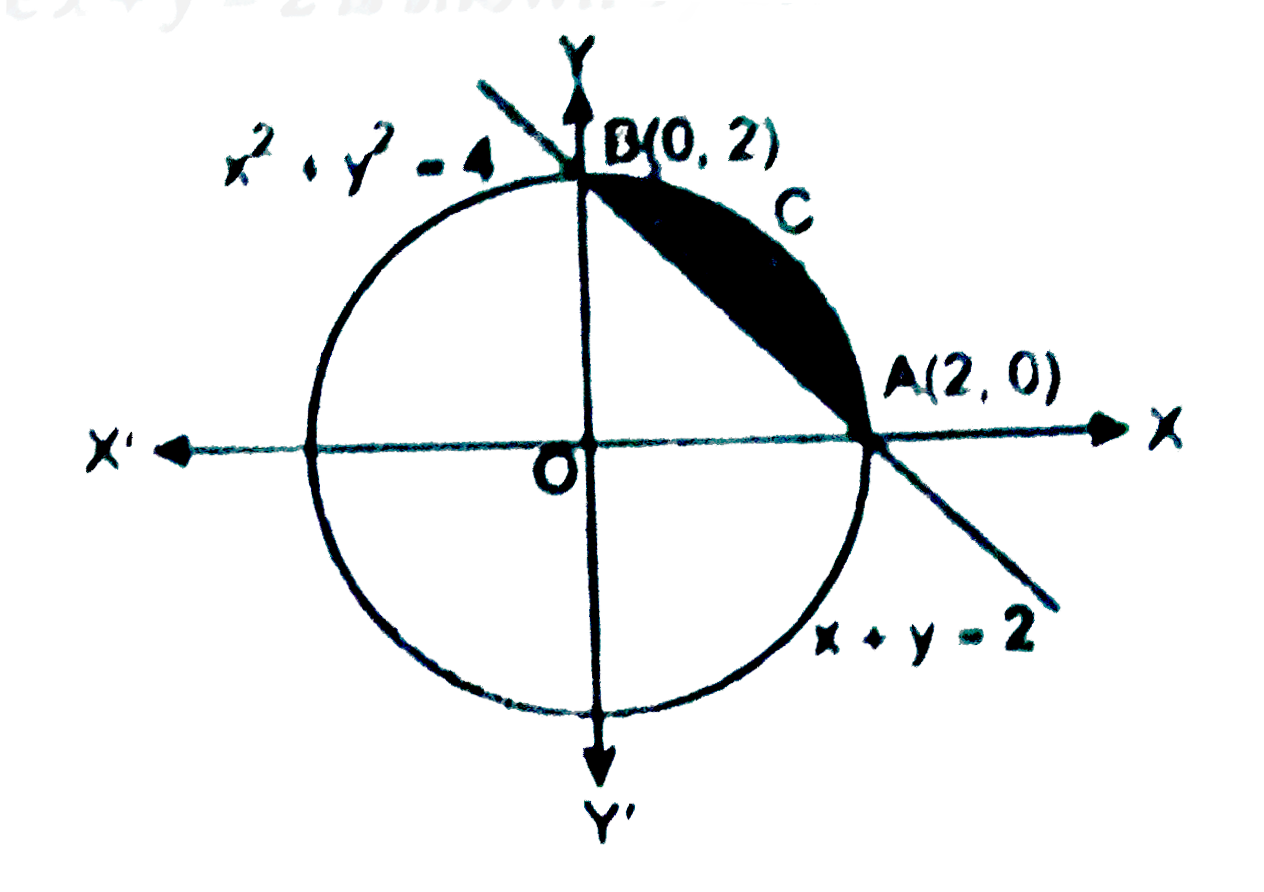A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
APPLICATIONS OF INTEGRALS
NAGEEN PRAKASHAN|Exercise Miscellaneous Exercise|19 VideosAPPLICATIONS OF INTEGRALS
NAGEEN PRAKASHAN|Exercise Exercise 8.1|13 VideosAPPLICATIONS OF DERIVATIVES
NAGEEN PRAKASHAN|Exercise Miscellaneous Exercise|24 VideosContinuity and Differentiability
NAGEEN PRAKASHAN|Exercise Miscellaneous Exercise|23 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Exercise 8.2
- Find the area of the circle 4x^2+4y^2=9which is interior to the parab...
Text Solution
|
- Find the area bounded by curves (x-1)^2+y^2=1 and x^2+y^2=1.
Text Solution
|
- Find the area of the region bounded by the curves y=x^2+2, y = x , x ...
Text Solution
|
- Using integration find the area of region bounded by the triangle who...
Text Solution
|
- Using integration find the area of the triangular region whose side...
Text Solution
|
- Smaller area enclosed by the circle x^2+y^2=4and the line x + y = 2is...
Text Solution
|
- Area lying between the curves y^2=4xand y = 2xis(A) 2/3 (B) 1/3 (C) ...
Text Solution
|