Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Miscellaneous Exercise
- Find the area under the given curves and given lines:(i) y=x^2,x = 1,...
Text Solution
|
- Find the area between the curves y = xand y=x^2.
Text Solution
|
- Find the area of the region lying in the first quadrant and bounded b...
Text Solution
|
- Sketch the graph of y = |x + 3|and evaluateint-6 0|x+3|dx.
Text Solution
|
- Find the area between the x-axis and the curve y=sinx from x=0 to x=2p...
Text Solution
|
- Find the area enclosed between the parabola y^2=4a xand the line y = ...
Text Solution
|
- Find the area enclosed by the parabola 4y=3x^2 and the line2y = 3x + ...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^2)/9+(y...
Text Solution
|
- Find the area of the smaller region bounded by the ellipse (x^2)/(a^2...
Text Solution
|
- Find the area of the region enclosed by the parabola x^2=y , the li...
Text Solution
|
- Using the method of integration find the area bounded by the curve |...
Text Solution
|
- Find the area bounded by curves {(x ,y):ygeqx^2 and y = | x |}
Text Solution
|
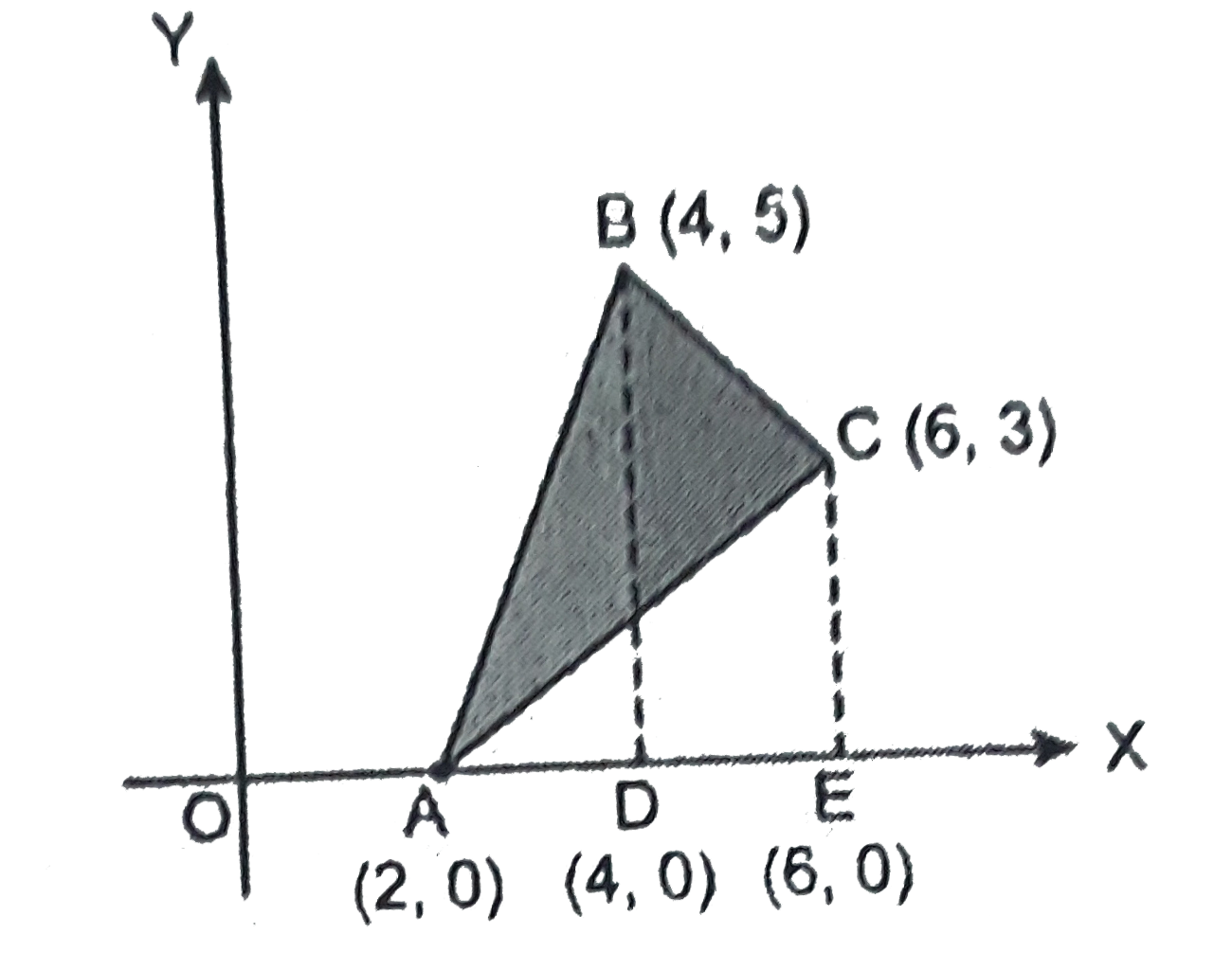
- Using the method of integration find the area of the triangle ABC, ...
Text Solution
|
- Using the method of integration find the area of the region bounded b...
Text Solution
|
- Find the area of the region {(x ,y): y^2lt=4x ,4x^2+4y^2lt=9}
Text Solution
|
- The area (in square units) bounded by the curve y=x^3, the x-axis and ...
Text Solution
|
- The area bounded by the curve y = x | x | , x-axis and the ordinates...
Text Solution
|
- The area of the circle x^2+y^2=16 exterior to the parabola y^2=6x is
Text Solution
|
- Find the area bounded by the y-axis, y=cosx ,a n dy=sinxw h e n0lt=xlt...
Text Solution
|