Text Solution
Verified by Experts
Topper's Solved these Questions
THERMODYNAMICS
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|24 VideosTHERMODYNAMICS
SUBHASH PUBLICATION|Exercise THREE MARK QUESTIONS AND ANSWERS|3 VideosTHERMAL PROPERTIES OF MATTER
SUBHASH PUBLICATION|Exercise FOUR MARKS QUESTIONS AND ANSWERS|22 VideosUNITS AND MEASUREMENTS
SUBHASH PUBLICATION|Exercise NUMERICALS WITH SOLUTIONS|13 Videos
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-THERMODYNAMICS-FIVE MARKS QUESTIONS WITH ANSWERS
- Derive Mayer's equation from the I law of thermodynamics.
Text Solution
|
- Show that for an isotheremal process, work W=muRTlog(e)((V(2))/(V(1)))...
Text Solution
|
- Distinguish between isothermal and adiabatic processes.
Text Solution
|
- Obtain an expression for the work done in a adiabatic process.
Text Solution
|
- Show that efficiency of Caront's ideal heat engine is eta=(1-(T(2))/(T...
Text Solution
|
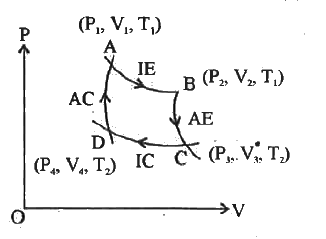
- Explain the working of Carnot's heat engine with the help of graph.
Text Solution
|