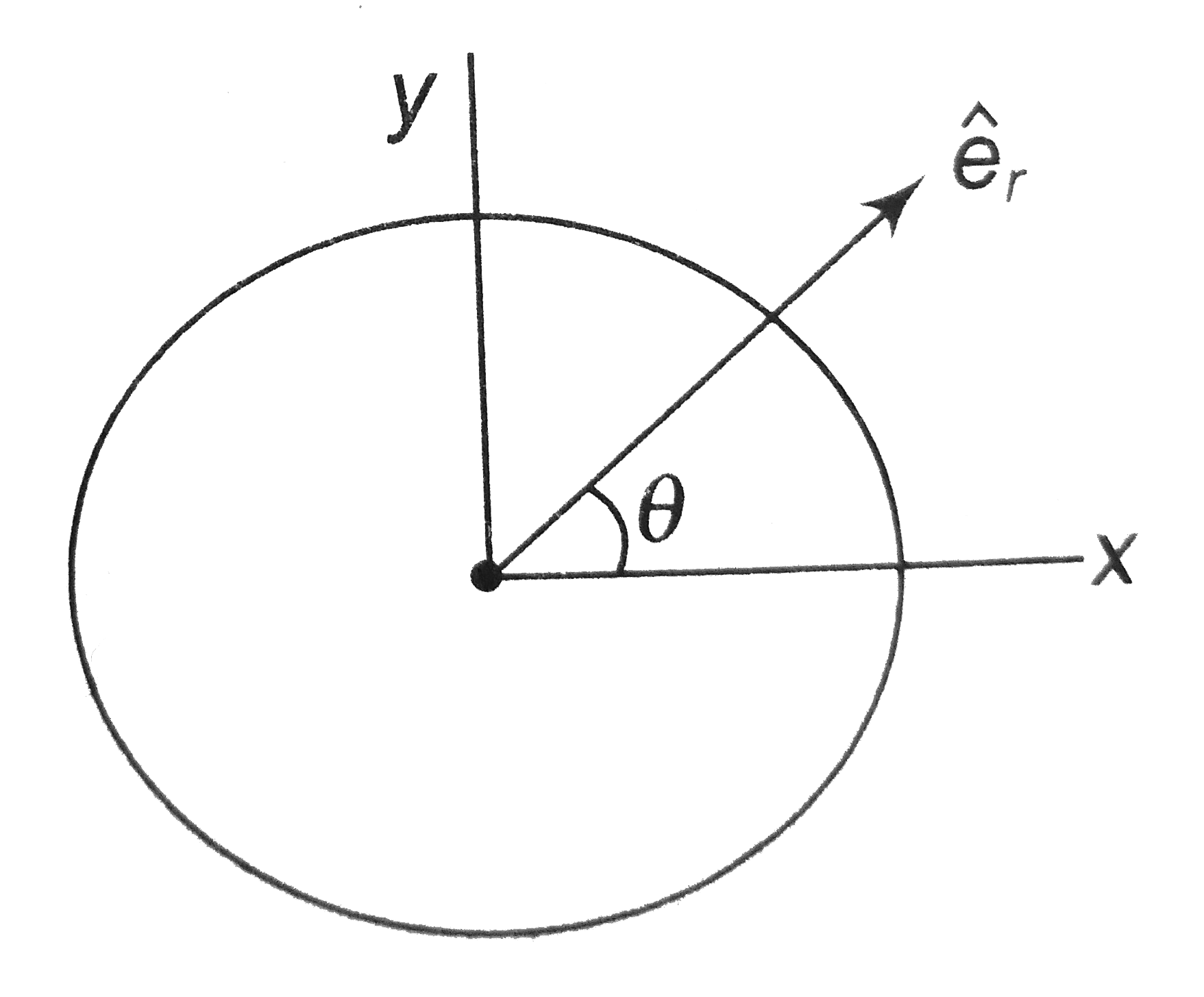
`hat(e )_(r)` is unit Vector along radius of a circle shown in figure `hat(e )_(r)` can be represented as `

The unit vector along hat(i)+hat(j) is

If hat(i) denotes a unit vector along incident light ray, hat( r) a unit vector along refracted ray into a medium of refractive index mu and hat(n) unit vector normal to boundary of medium directed towards incident medium, then law of refraction is

If hat(i) denotes a unit vector along incident light ray, hat (r) a unit vector along refracted ray into a medium of refraction index mu and hat (n) unit vector normal to boundary of medium directed towards incident medium, then law of refraction is

If hat(i) denotes a unit vector along incident light ray, hat( r) a unit vector along refracted ray into a medium of refractive index mu and hat(n) unit vector normal to boundary of medium directed towards incident medium, then law of refraction is

The unit vector along vec(A)= 2 hat i + 3 hat j is :

The unit vector along vec(A)= 2 hat i + 3 hat j is :

Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates A=A_(x)hat(i) + A_(y)hat(j) , where hat(i) and hat(j) are unit vector along x and y-directions, respectively and A_(x) and A_(y) are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as A= A_(r)hat(r) + A_(theta) hat(theta) , where hat(r)=(r)/(r)=cos theta hat(i)+sin theta hat (j) and hat(theta)=-sin theta hat(i) + cos theta hat (j) are unit vectors along direction in which r and theta are increasing. (a) Express hat(i) and hat (j) in terms of hat(r) and hat (theta) . (b) Show that both hat(r) and hat(theta) are unit vectors and are perpendicular to each other. (c) Show that (d)/(dt)(hat(r))= omega hat(theta) , where omega=(d theta)/(dt) and (d)/(dt) (hat(theta))=-thetahat(r) . (d) For a particle moving along a spiral given by r=a theta hat(r) , where a = 1 (unit), find dimensions of a . (e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.

A unit vector along the direction hat(i) + hat(j) + hat(k) has a magnitude :

(a) Derive an expression for unit vector along reflected ray (hat r) if unit vectors hat i and hat n represents unit vectors along incident light ray and normal (at point of reflection and outward from surface) respectively. (b) If vector along the incident ray on a mirror is -2 hat i+ 3 hat j + 4 hat k . Considering the x-axis to be along the normal. Then, find the unit vector along the reflected ray.