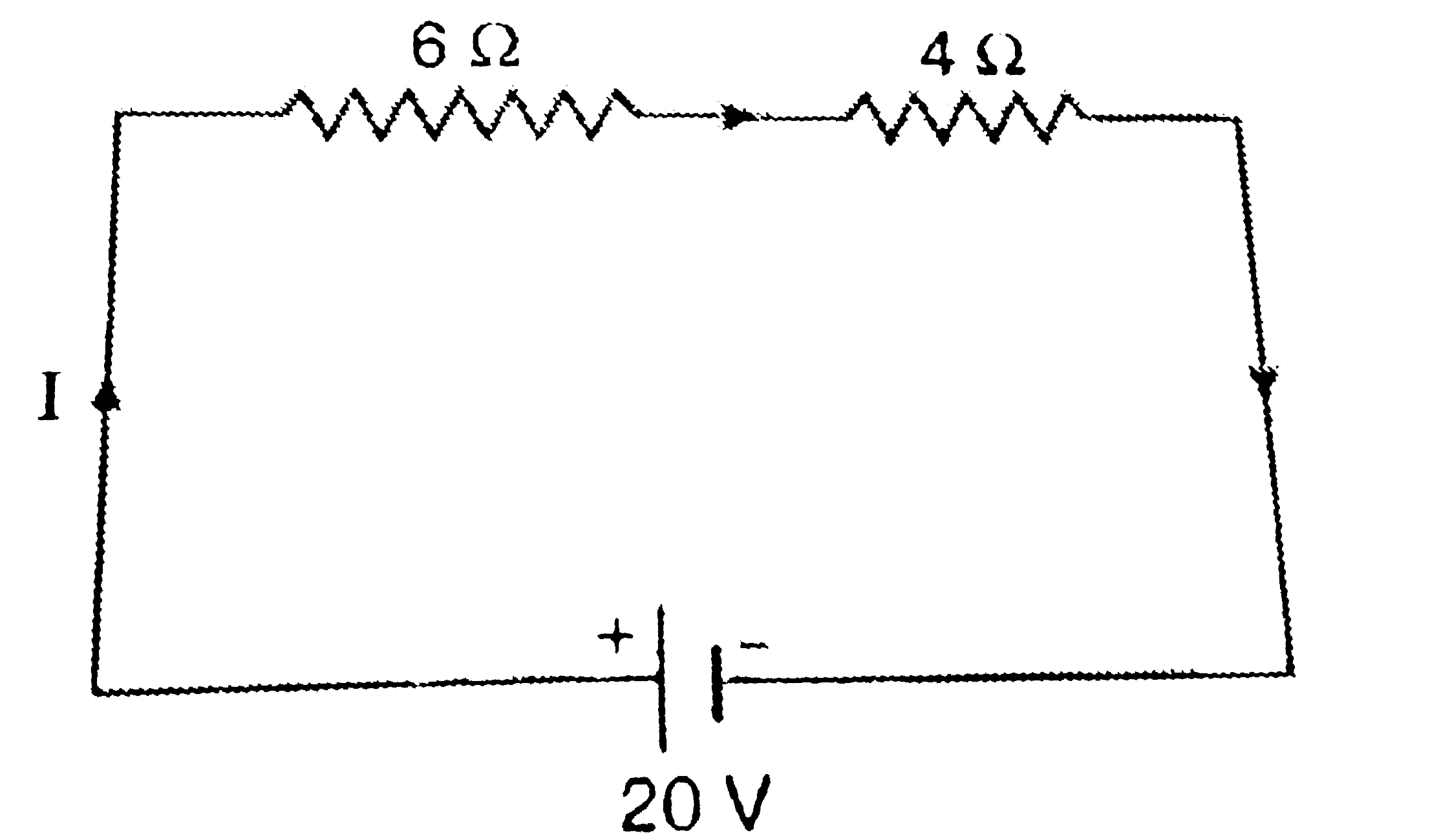
The first step in solving such problems based on current electricity is to draw a proper circuit diagram. For example, in this problem we have two resistances of 6 ohms and 4 ohms which are connected in series. So, first of all we have to draw these two resistances on paper as shown in Figure alongside. Now, a potential difference of 20 volts has been applied across this combination of resistances. So, we draw a cell or a battery of 20 volts and complete the circuit as shown in Figure alongside. Suppose the current flowing in the circuit is I amperes.
We will now find out the value of current I flowing through the circuit. To do this we should know the total resistance R of the circuit. Here we have two resistance of `6 Omega` and `4 Omega` connected in series. So,
Total resistance, `R = R_(1) +R_(4)`
`R = 6+4`
`R = 10` ohms
Now, Total resistance, `R = 10` ohms
Potential difference, `V = 20` volts
and, Current in the circuit, `I = ?` (To be calculated)
So, applying Ohm's law to the whole circuit, we get:
`(V)/(I) = R`
So that, `(20)/(I) = 10`
And, `10 I = 20`
`I = (20)/(10)`
So, Current, `I = 2` amperes (or 2A)
Thus, the current flowing through the circuit is 2 amperes. The second part of this problem is to find out the potential difference across the ends of the 6 ohms resistance. To do this we will have to apply Ohm's law to this resistance only. We know that the current flowing through the 6 ohm resistance will also be 2 amperes. Now,
Potential difference (across `6 Omega` resistance), `V = ?` (To be calculated)
Current (through `6Omega` resistance), `I = 2` amperes
And, Resistance, `R = 6` ohms
So, applying Ohm's law to the `6Omega` resistance only, we get:
`(V)/(I) = R`
or `(V)/(2) = 6`
So, Potential difference, `V = 12 `volts
Thus, the potential difference across the 6 ohm resistance is 12 volts.