Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
SUBHASH PUBLICATION-ANNUAL EXAM QUESTION PAPER -MARCH -2017 -PART -D
- Deduce the condition for balance of a wheatstone's bridge using...
Text Solution
|
- Derive the expression for magnetic field at a point on the axis of a c...
Text Solution
|
- Write any five properites of ferromagnetic materials
Text Solution
|
- Derive th lens maker's formula.
Text Solution
|
- State the law of radioactivity and hence, show that N=N(0)e^(-lambda ...
Text Solution
|
- What is rectification with relevant circuit diagram and waveform exp...
Text Solution
|
- Two point charges q(A)=3muC and q(B)=-3muC are located 0.2 m apart in ...
Text Solution
|
- Two point charges q(A)=3muC and q(B)=-3muC are located 0.2 m apart in ...
Text Solution
|
- Which two resistors are connected in series with a cell of emf 2V and ...
Text Solution
|
- A source of alternating emf of 220 V-50 Hz is connected in series wit...
Text Solution
|
- Light of wavelength 6000 overset(@)A is used to obtain interference fr...
Text Solution
|
- The first member of the Balmer series of hydrogen atom has wavelength ...
Text Solution
|
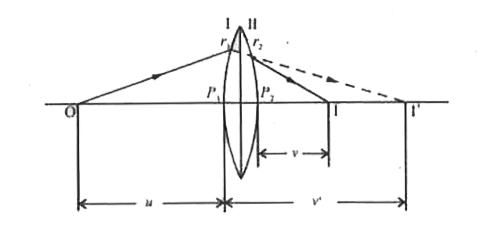 Let `r_(1) and r_(2)` be the radii of curvature of the thin lens .
Let `r_(1) and r_(2)` be the radii of curvature of the thin lens .