Similar Questions
Explore conceptually related problems
Recommended Questions
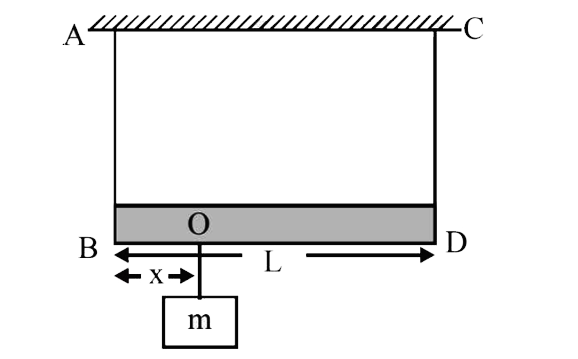
- A massless rod of length L is suspened by two identical string AB and ...
Text Solution
|
- Two lines A B and C D intersect at O such that B C is equal and parall...
Text Solution
|
- Two lines A B\ a n d\ C D intersect at O such that B C is equal and pa...
Text Solution
|
- A massless rod of length L is suspened by two identical string AB and ...
Text Solution
|
- A massless rod BD is suspended by two identical massless strings AB an...
Text Solution
|
- The length of two chords AB and CD of a circle with its centre ...
Text Solution
|
- A massless rod is suspended by two identical strings AB and CD of equa...
Text Solution
|
- A massless rod BD is suspended by two identical massless strings AB an...
Text Solution
|
- एक द्रव्यमान छड़ BD को एक जैसी द्रव्यमानहीन डोरियों AB तथा CD द्वार...
Text Solution
|