Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CPC CAMBRIDGE PUBLICATION-TRIANGLES -EXERCISE 5.3
- triangleABC and triangleDBC are two isosceles triangles on the same ba...
Text Solution
|
- AD is an altiude of an isosceles triangle ABC in which AB = AC. Show t...
Text Solution
|
- Two sides AB and BC and median AM of one triangle ABC are respectively...
Text Solution
|
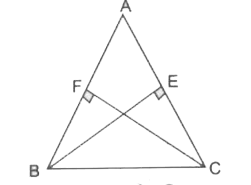
- BE and CF are two altitudes of a triangle ABC. Using RHS congruence ru...
Text Solution
|
- ABC is an isosceles triangle with AB = AC. Draw AP bot BC to show that...
Text Solution
|