Home
Class 9
MATHS
In a triangle, locate a point in its int...

In a triangle, locate a point in its interior of which is equidistant from all the sides of triangle.

Text Solution

Verified by Experts

The correct Answer is:
PI = QI = RI
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    CPC CAMBRIDGE PUBLICATION|Exercise EXERCISE 5.4|6 Videos

  • SURFACE AREAS AND VOLUMES

    CPC CAMBRIDGE PUBLICATION|Exercise EXERSICE 13.8|10 Videos

Similar Questions

Explore conceptually related problems

ABC is triangle. Locate a point in the interior of Delta ABC which is equidistant from all the vertices of Delta ABC .

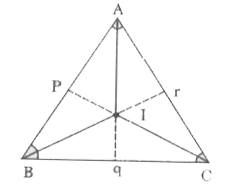
ABC is a triangle . Locate a point in the interior of triangleABC which is equidistant from all the vertices of triangleABC .

The locus of the points which are equidistant from (-a, 0) and x=a

To construct a triangle similar to a given triangle ABC with its sides (8)/(5) th the corresponding sides of triangle A, B, C draw a ray BX such that CBX is an acute angle and X is on the opposite side of A with respect to BC. The minimum number of points to be located at equal distances on the ray BX

The perimeter of angled triangle is 30 cm and its hypotenuse is 13 cm. Find the length of other two sides of triangle.

Prove that the area of an equilateral triangle described on one side of a square is equal of half the area of the equilateral triangle described on one of its diagonals.

The sides AB, BC BC, CA of triangles ABC have 3 4 and 5 interior points respectively on them . The toal number of triangles that can be constructed by using these points as vertices is :

To construct a triangle similar to a given triangle ABC with its sides (3^(th) )/(7) the corresponding sides of triangle ABC, first draw a ray BX such that CBX is an acute angle and X lies on the opposite side of A with respect to BC. Them, locate points B_1, B_2, B_3, ... on BX at equal distance and the next step is to join

Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.