Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CPC CAMBRIDGE PUBLICATION-QUADRILATERALS-EXERCISE 7.2
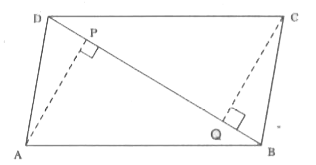
- ABCD is a parallelogram and AP and CQ are perpendicular from vertices ...
Text Solution
|
- ABCD is a quadrilateral in which P,Q,R and S are mid points of the sid...
Text Solution
|
- ABCD is a rhombus and P,Q,R and S are the mid points of the sides AB,B...
Text Solution
|
- ABCD is a rectangle and P,Q,R and S are the mid points of the sides AB...
Text Solution
|
- ABCD is a trapezium in which AB||DC, BD is a diagonal and E is the mid...
Text Solution
|
- In a parallelogram ABCD, E and F are the mid points of sides AB and CD...
Text Solution
|
- Show tha the line segments joining the mid points of the opposite side...
Text Solution
|
- ABC is a triangle right angled at C. A line through the mid points M o...
Text Solution
|