Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CPC CAMBRIDGE PUBLICATION-CIRCLES -EXERCISE 12.6
- Prove that the line of centres of two intersecting circles subtends eq...
Text Solution
|
- ABCD is a parallelogram. The circle through A, B and C intersect CD (p...
Text Solution
|
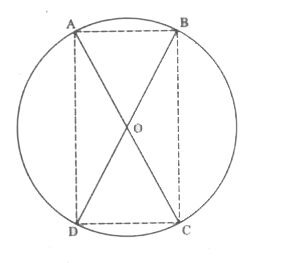
- AC and BD are chords of a circle which bisect each other. Prove that ...
Text Solution
|
- Two congruent circles intersect each other at points A and B. Through ...
Text Solution
|